66 Московская математическая олимпиада. 10 класс.

Олимпиада состоялась 2 марта 2003 года, на выполнение задания отводилось 5 астрономических часов.

Задачи

1. Существуют ли такие натуральные числа a, b и c, что у каждого из уравнений
ax²+bx+c=0,
ax²+bx-c=0,
ax²-bx+c=0,
ax²-bx-c=0
оба корня - целые?

2. По рёбрам выпуклого многогранника с 2003 вершинами проведена замкнутая ломаная, проходящая через каждую вершину ровно один раз. Докажите, что в каждой из частей, на которые эта ломаная делит поверхность многогранника, количество граней с нечётным числом сторон нечётно.

3. Пусть P(x) - многочлен со старшим коэффициентом 1, а последовательность целых чисел a₁, a₂, ... такова, что P(a₁)=0, P(a₂)=a₁, P(a₃)=a₂ и т. д. Числа в последовательности не повторяются. Какую степень может иметь P(x)?

4. Пусть M - точка пересечения медиан в DABC. На перпендикулярах, опущенных из M на стороны BC, AC и AB, взяты точки A₁, B₁ и C₁ соответственно, причём A₁B₁ | MC и A₁C₁ | MB. Докажите, что M является точкой пересечения медиан и в DA₁B₁C₁.

5. В стране несколько городов, соединённых дорогами с односторонним и двусторонним движением. Известно, что из каждого города в любой другой можно проехать ровно одним путём, не проходящим два раза через один и тот же город. Докажите, что страну можно разделить на три губернии так, чтобы ни одна дорога не соединяла два города из одной губернии.

6. Дана бесконечная последовательность многочленов P₁(x), P₂(x), ... . Всегда ли существует конечный набор функций f₁(x), f₂(x), ..., f_N(x), композициями которых можно записать любой из них (например, P₁(x)=f₂(f₁(f₂(x))))?

Решения

1. Ответ: да, например, a=1, b=5, c=6.

Решение. Можно считать, что a=1, поскольку если x₁ и x₂ - корни уравнения ax²+bx+c, то b=-(x₁+x₂)a, c=x₁x₂a, т. е. все коэффициенты уравнения можно сократить на a. Заметим также, что корни уравнений, отличающихся только знаком при bx, противоположны, поэтому достаточно лишь того, чтобы корни уравнений x²+bx+c=0 и x²+bx-c=0 были целыми.

Для того, чтобы это выполнялось, необходимо, чтобы дискриминанты этих уравнений были точными квадратами: b²-4c=m², b²+4c=n². Это же условие оказывается и достаточным - ведь b²-4c той же чётности, что и b, а значит и (b²-4c)^1/2 (если этот корень целый) оказывается той же чётности. Тем самым, x_1,2=(-b+(b²-4c)^1/2)/2 (корни уравнения x²+bx+c=0) - целые числа. Аналогично для второго уравнения.

На самом деле, таких b, c, m, n существует бесконечно много. Для решения задачи достаточно предъявить один пример таких b, c, m, n. Покажем, как такой пример можно было подобрать. Исключая c, получаем n²-b²=b²-m², при этом, чтобы c было целым необходимо, чтобы b, m и n были одной чётности. Перебрав квадраты нечётных чисел от 1 до 9, находим одно из решений: 7²-5²=5²-1=24; c=24/4=6. Мы нашли b и c, такие что дискриминанты обоих уравнений - полные квадраты.

Для того, чтобы найти пример, нам потребовалось подобрать представление 2b² в виде суммы m²+n², отличное от b²+b². Мы нашли такие b, m и n просто подбором, но в действительности задача представления заданного числа в виде суммы двух квадратов хорошо изучена. Она связана с так называемыми гауссовыми целыми числами - числами вида x+y(-1)^1/2, где x и y - целые. В частности, можно доказать, что нетривиальное представление 2b²=m²+n² существует тогда и только тогда, когда в разложении b на простые множители входит хотя бы одно простое число вида 4k+1. Подробнее об этом можно прочитать, например, в статье В. Сендерова и А. Спивака "Суммы квадратов и целые гауссовы числа" (Квант, 1999, N 3, стр. 14-22).

2. Выберем любую из получившихся частей. Рассмотрим сумму a₁+a₂+...+a_n, где a_i - количество сторон i-й грани.

Каждое ребро многогранника, по которому ломаная не проходит, посчитано в этой сумме дважды и поэтому чётность суммы не зависит от числа таких рёбер. Каждое ребро, через которое проходит ломаная, входит в сумму ровно один раз. Таких рёбер 2003, поэтому вся сумма нечётна.

Если бы количество граней с нечётным числом сторон было чётно, то рассмотренная сумма также была бы чётна. Значит, это количество нечётно.

3. Ответ: степень многочлена может равняться только 1.

Решение. Если степень многочлена P(x) равна 0, то P(x)=1 (старший коэффициент равен 1). Но тогда уравнение P(a₁)=0 не имеет решения. Если степень многочлена равна 1, то, например, многочлен P(x)=x-1 и последовательность 1, 2, 3, ... (a_n=n) удовлетворяют условию задачи.

Докажем, что нет таких многочленов степени 2 и выше. Можно показать (см. ниже), что найдётся положительная константа C (для каждого многочлена - своя), что если |x|>C, то |P(x)|>|x|. Заметим теперь, что все члены последовательности по модулю ограничены C. Действительно, если |a_n|>C, то C<|a_n|<|P(a_n)|=|a_n-1|. Продолжая, получим:

C<|a_n|<|P(a_n)|=|a_n-1|<|P(a_n-1)|<...<|P(a₂)|=|a₁|<|P(a₁)|=|0|,

что неверно.

Теперь мы получим, что последовательность состоит из целых чисел, по модулю не превосходящих C, а их конечное число, т. е. в последовательности обязательно будут повторения.

Осталось обосновать существование такой константы C. Для многочлена
P(x)=xⁿ+b_n-1x^n-1+...+b₂x²+b₁x+b₀
можно взять
C=|b_n-1|+...+|b₁|+|b₀|+1.

Действительно, если |x|>C, то

|P(x)|>|x|ⁿ-(|b_n-1|*|x|^n-1+...+|b₁|*|x|¹+|b₀|)>
>|x|ⁿ-(|b_n-1|*|x|^n-1+...+|b₁|*|x|^n-1+|b₀|*|x|^n-1)=
=|x|^n-1*(|x|-(|b_n-1|+...+|b₀|))>|x|^n-1>|x|.

4. Первое решение. Обозначим

BC=a,   CA=b,   AB=c,
MA'=x,   MB'=y,   MC'=z.
(жирным шрифтом обозначены векторы)

Тогда условие задачи записывается так:

(c,z)=(a,x)=(b,y)=0,       (1)
((y-z),(b-c))=((x-z),(a-c))=0.      (2)

Раскрывая в (2) скобки и учитывая (1), получим (b,z)+(c,y)=(a,z)+(c,x)=0. Поскольку c=-a-b, имеем: (b,z)-(a,y)=(a,z)-(b,x)=0.

Нужно доказать, что x+y+z=0, для чего достаточно, чтобы (a,(x+y+z))=(b,(x+y+z))=0.
Действительно, (a,(x+y+z))=(a,y)+(a,z)=(a,y)+((-c-b),z)=-(b,z)+(a,y)=0.
Аналогично, (b,(x+y+z))=(b,x)+(b,z)=(b,x)+(-c-a),z)=-(a,z)+(b,x)=0.

Второе решение. Для равностороннего треугольника утверждение задачи тривиально. Сведём задачу к случаю равностороннего треугольника.

Точки A', B' и C' задаются следующими условиями:

MA' | BC,   MB' | AC,   MC' | AB,   A'B' | MC,   A'C' | MB.

Повернём треугольник A'B'C' вокруг точки M на 90^o против часовой стрелки. Условия на точки A', B' и C' перейдут в следующие:

MA'||BC,   MB'||AC,   MC'||AB,   A'B'||MC,   A'C'||MB.

При этом задача перейдёт в равносильную. Проведём аффинное преобразование, переводящее треугольник ABC в равносторонний. Задача снова перейдёт в равносильную, поскольку выражается только через параллельность, пересечение прямых и середины.

Теперь повернем треугольник A'B'C' по часовой стрелке на 90^o. Задача перейдёт в исходную, но с равносторонним треугольником ABC.

5. Пусть внутри страны, пока ещё не поделённой на губернии, возникла автономная область, состоящая из одного города. Эту область, во-первых, можно разделить на три губернии (две пустые), и во-вторых, она удовлетворяет условию как самостоятельная страна, т. е. при удалении всех остальных городов. Будем добавлять города к автономной области с сохранением этих двух условий.

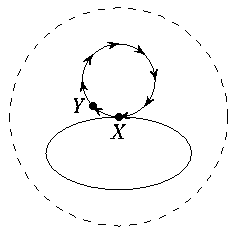
Рис. 25

Предположим, что область содержит не все города. Тогда найдётся дорога, ведущая из города области (обозначим его через X) в город, ещё не принадлежащий автономной области (назовём его Y). Рассмотрим несамопересекающийся путь (последовательность дорог), ведущий из Y в X (рис. 25).

Докажем, что на этом пути не встретятся города области, кроме разве что последнего города X. Предположим обратное: на этом пути есть город Z, лежащий в автономной области. Тогда из X можно добраться до Z двумя несамопересекающимися путями: один путь идёт через Y, а второй идёт только по городам области (такой путь существует, потому что для области выполнено условие задачи, как и для всей страны). Но по условию такое невозможно. Следовательно, путь из Y в X не содержит других городов из области, кроме X.

Теперь присоединим все города на этом пути (включая Y) к автономной области и отнесём их поочерёдно в те две губернии, в которые X не входит. Все дороги, соединяющие два присоединённых города - это дороги на пути Y->X, иначе между ними было бы два пути. Аналогично, все дороги, соединяющие присоединённый город с городом, уже имевшимся в области - это дорога из X в Y и последняя дорога на пути Y->X. Следовательно, область будет правильно разделена на губернии.

Докажем, что для новой области условие задачи также выполнено. Два несамопересекающихся пути от одного города к другому невозможны, иначе бы вся страна не удовлетворяла условию. От каждого города области можно доехать (по области) до X, а от X - до всех остальных, поэтому по крайней мере один путь от одного города области до другого всегда существует. Значит, новая область тоже удовлетворяет условию.

На каждом описанном шаге область увеличивается хотя бы на один город (Y). Следовательно, рано или поздно все города будут присоединены. В этот момент область совпадёт со всей страной и при этом будет разделена на губернии. Таким образом, утверждение задачи доказано.

6. Ответ: это возможно.

Решение. Пусть, например,
f(x)=p+arctg x,
g(x)=x+p,
h(x) - функция, которая на интервале (-(p/2)+pn; (p/2)+pn) равна P_n(tg x)   (рис. 26).
Тогда

P_n(x)=h(g(g(...(g(f(x)))...)))
(функция g используется (n-1) раз).

Пояснение. Сопоставим каждой паре (x, n), где n - натуральное число, а x - действительное, некоторое число A(x,n) таким образом, чтобы числа A(x,n) не совпадали для любых двух различных пар.

Для этого разобьём действительную ось на интервалы (-(p/2)+pk, (p/2)+pk). Каждому номеру n сопоставим интервал (-(p/2)+pn, (p/2)+pn), каждой паре (x, n) - соответственно число из интервала (-(p/2)+pn, (p/2)+pn), равное A(x,n)=arctg x+pn.

Функции f, g, h таковы, что
f(x)=A(1, x)
g(A(n, x)=A((n+1), x)
h(A(n, x)=P_n(x) (см. рис. 26).

Тогда h(g(g(...(g(f(x)))...)))   (функция g используется (n-1) раз), очевидно, равно P_n(x).

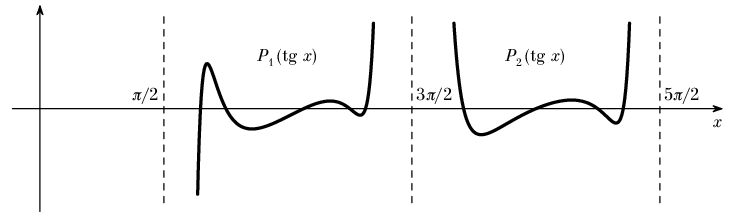
Рис. 26