
Рис. 11
Олимпиада состоялась 2 марта 2003 года, на выполнение задания отводилось 5 астрономических часов.
1. В семье 4 человека. Если Маше удвоят стипендию, общий доход всей семьи возрастет на 5%, если вместо этого маме удвоят зарплату - на 15%, если же зарплату удвоят папе - на 25%. На сколько процентов возрастет доход всей семьи, если дедушке удвоят пенсию?
2. Придумайте десятизначное число, в записи которого нет нулей, такое что при прибавлении к нему произведения его цифр получается число с таким же произведением цифр.
3. Можно ли покрасить некоторые клетки доски 8*8 так, чтобы в любом квадрате 3*3 было ровно 5 закрашенных клеток, а в каждом прямоугольнике 2*4 (вертикальном или горизонтальном) - ровно 4 закрашенные клетки?
4. В треугольнике ABC на сторонах AC и BC взяты точки X и Y такие, что /ABX = /YAC, /AYB = /BXC, XC=YB. Найдите углы треугольника ABC.
5. В стране 15 городов, некоторые из них соединены авиалиниями, принадлежащими трем авиакомпаниям. Известно, что даже если любая из авиакомпаний прекратит полеты, можно будет добраться из любого города в любой другой (возможно, с пересадками), пользуясь рейсами оставшихся двух компаний. Какое наименьшее количество авиалиний может быть в стране?
6. Боря задумал целое число, большее чем 100. Кира называет целое число, большее чем 1. Если Борино число делится на это число, Кира выиграла, иначе Боря вычитает из своего числа названное, и Кира называет следующее число. Ей запрещается повторять числа, названные ранее. Если Борино число станет отрицательным - Кира проигрывает. Есть ли у нее выигрышная стратегия?
1. Ответ: 55%.
Решение. Если Маше удвоят стипендию, семейный доход возрастёт на размер этой стипендии. Следовательно, Машина стипендия составляет 5% общего дохода. Аналогично, мамина зарплата составляет 15%, а папина - 25%. Оставшаяся доля 100%-5%-15%-25%=55% приходится на дедушкину пенсию. Значит, если ему удвоят пенсию, доход всей семьи возрастёт на 55%.
Это же решение можно сформулировать по-другому. Если бы всем членам семьи вдруг стали платить вдвое больше, общий доход увеличился бы на 100%. Из этих 100 процентов 5 приходится на Машу, 15 - на маму, 25 - на папу, а остальные 55 - на дедушку.
2. Ответ: например, 1111111613.
Решение. Сперва найдём какое*нибудь число, удовлетворяющее условию задачи, не обязательно десятизначное. Например, попробуем найти такое число, что после прибавления к нему произведения цифр они попросту меняются местами. Если последние цифры числа - 13, то, чтобы поменять их местами, нужно прибавить 18. Чтобы произведение цифр было 18, нужно дописать ещё цифру 6. Искомым является число 613: 613+6*1*3=631. Другие аналогичные числа: 326+3*2*6=362, 819+8*1*9=891 и т. п.
В наименьшем известном примере - 28+2*8=44 - цифры изменяются, однако их произведение сохраняется! Другой пример: 214+2*1*4=222.
Теперь, чтобы получить десятизначное число, припишем слева недостающее число единиц. Произведение цифр от этого не изменится. Например, 1111111613+18=11111111631. Также можно приписать в начало и конец равное число двоек и пятёрок, например, 5555282222+10*10*10*10*16=5555442222.
Другие интересные примеры, встретившиеся в работах школьников: 1111159121, 1111954511, 1111332123, 1111113148, 2356478911, 1111553431, 1952219522, 1231451671, 3355211211, 5132486791.
3. Ответ: нельзя.
Решение. Предположим, что такая раскраска возможна. На всех рисунках не заштрихованы клетки, про которые выяснено, что они не закрашены; штриховкой обозначены клетки, про которые ещё не известно, закрашены они или нет; двойной штриховкой - заведомо закрашенные.

Рис. 11
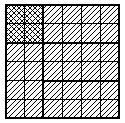
Доску 8*8 можно разрезать на восемь прямоугольников 4*2, поэтому на ней ровно 8*4=32 закрашенные клетки.
Также её можно разрезать на четыре квадрата 3*3, три прямоугольника 4*2 и угловой квадратик 2*2 (рис. 11). В четырёх квадратах 3*3 и трёх прямоугольниках 4*2 уже 4*5+3*4=32 клетки, поэтому в угловом квадратике 2*2 не должно быть ни одной закрашенной клетки. Аналогично можно доказать, что и в остальных угловых квадратиках 2*2 нет закрашенных клеток.

Рис. 12
Доску без угловых квадратиков 2*2 можно разрезать на шесть прямоугольников 4*2 (рис. 12). Получаем, что всего на доске 6*4=24 закрашенные клетки. Противоречие.
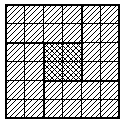
Примечание. Доказав, что угловые квадратики 2*2 не закрашены, можно действовать и по-другому, например, так. Разместим на доске четыре квадрата 3*3 и два прямоугольника 4*2 как показано на рис. 13. На оставшееся место приходится 32-(4*5+2*4)=4 закрашенные клетки, и туда можно поместить два прямоугольника 4*2, перекрывающиеся по квадратику 2*2. В каждом из них четыре закрашенные клетки, и вместе у них четыре закрашенных клетки - значит, закрашено их пересечение, и угловой квадратик 2*2 должен быть полностью закрашен. Противоречие.
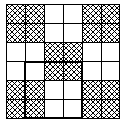
Приведём ещё одно решение. Покажем, что даже доску 6*6 нельзя раскрасить указанным в задаче образом. Так как её можно разрезать на четыре квадрата 3*3, в ней должно быть ровно 4*5=20 закрашенных клеток. Разрежем её на четыре прямоугольника 4*2 и квадратик 2*2 (рис. 14). В этих прямоугольниках 4*4=16 клеток, значит в 2*2 сосредоточены остальные 20-16=4 клетки, т. е. все клетки в нём закрашены.

Рис. 13
Переложив четыре прямоугольника другим образом, можно то же самое доказать про квадратики 2*2 в других углах, а также про квадратик в центре (рис. 15). Остальные клетки должны быть незакрашенными, так как в каждом прямоугольнике 4*2 уже есть по четыре закрашенные клетки. Теперь легко указать квадрат 3*3, в котором всего четыре закрашенные клетки (рис. 16).
 |  |  |
| Рис 14. | Рис 15. | Рис 16. |
4. Ответ: треугольник равносторонний, все углы по 60o.
Решение. Для внешних углов BXC и AYB треугольников ABX и CAY запишем равенства
/BXC = /ABX + /BAX,
/AYB = /CAY + /YCA
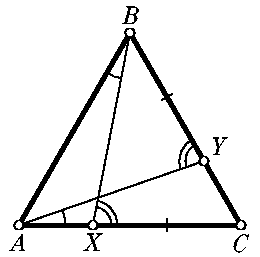
Рис. 17
Рассмотрим треугольники XBC и YAB. У них равны две стороны и угол не между ними: /BXC=/AYB, XC=YB, BC=AB. Такие треугольники либо равны, либо /XBC+/YAB=180o (мы докажем это ниже), но второй случай невозможен, поскольку /XBC+/YAB</ABC+/CAB=180o-/ACB<180o. Значит, DXBC=DYAB, а следовательно, /ABC=/BCA, и треугольник ABC равносторонний.
Теперь докажем сформулированный выше факт. Итак, в треугольниках XBC и YAB равны две стороны и угол не между ними: /BXC=/AYB, XC=YB, BC=AB. Отметим на луче XB точку B' на расстоянии XB'=YA. Точка B' может оказаться как внутри, так и вне отрезка XB (рис. 18, а, б). Треугольники XB'C и YAB равны по двум сторонам и углу между ними (XC=YB, XB'=YA, /CXB'=/BYA). Тогда CB'=CB. Если B и B' совпадают, треугольники XBC и YAB равны. Если же B' не совпадает с B, то в равнобедренном треугольнике B'CB углы B'BC и BB'C равны, а значит, /XBC+/XB'C=180o, и /XBC+/YAB=180o.
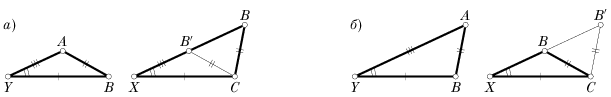
Рис. 18
5. Ответ: 21 авиалиния.
1) Докажем, что меньше, чем 21 линией не обойтись. Вначале докажем, что если 15 городов соединены авиалиниями так, что можно добраться от любого города до любого другого, то авиалиний не меньше 14.
Обозначим число авиалиний через k. Если мы уберём одну из них, города могут распасться на две разрозненные группы, между которыми нет воздушного сообщения, а могут и не распасться. После удаления следующей авиалинии не более одной группы может распасться ещё на две, количество разрозненных групп увеличится не более чем на одну. Продолжая аналогичные рассуждения, получим, что после удаления последней авиалинии количество разрозненных групп не может превысить k+1. Поскольку 15 городов без авиалиний - это 15 групп, то k>14.
Обозначим количество линий у авиакомпаний через a, b и c. По доказанному, у любых двух компаний вместе не менее 14 линий, т. е. a+b>14, b+c>14, c+a>14. Складывая эти неравенства, получаем: 2(a+b+c)>42, т. е. у трёх компаний в сумме не менее 21 авиалинии.
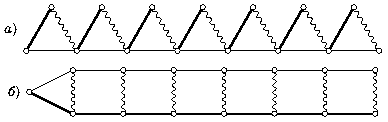
Рис. 19
2) Осталось привести пример с 21 авиалинией. Годится любой из примеров, показанных на рис. 19, а, б.
6. Ответ: есть.
Приведём стратегию игры за Киру. Сперва ей следует назвать "2". Если Боря не проиграл, то его число было нечётным. После вычитания двойки оно нечётным и останется.
Теперь Кире следует назвать "3". Чтобы понять, какие числа мы "отсеяли" этим ходом, рассмотрим возможные остатки изначального Бориного числа при делении на 6 (6=НОК(2,3) ). Если остаток был 0, 2 или 4, Кира выиграла бы первым ходом. Если остаток был 5, то после первого хода он стал бы 3, и Кира выиграла бы вторым ходом. Таким образом, игра будет продолжаться, если изначальное Борино число давало остаток 1 или 3 при делении на 6. После двух ходов из него вычтется 2+3=5, и его остаток при делении на 4 станет 2 или 4.
Третье число Киры - "4". Рассмотрим возможные остатки Бориного числа перед этим ходом при делении на 12 (12=НОК(2, 3, 4) ). Возможные остатки при делении на 6 - 2 или 4, а значит, при делении на 12 - 2, 4, 8 или 10. Игра будет продолжаться, если остаток был 2 или 10 (иначе разделится на 4), после вычитания 4 они превратятся соответственно в 10 и 6.
Четвёртое число Киры - "6". Если Борино число давало остаток 6 при делении на 12, оно разделится на 6, иначе после вычитания 6 останется единственный вариант - остаток "4". Кира называет "16", чтобы после вычитания 16 Борино число стало делится на 12. После этого можно называть "12", уж точно разделится! В табл. 1 представлены ходы Киры и те числа, которые могли быть у Бори в случае, если он не проигрывает на данном ходе; k означает произвольное натуральное число (в каждой клетке таблицы, вообще говоря, своё).
| Ход Киры | Возможное число Бори перед её ходом | Возможное число Бори после её хода |
| 2 | любое | 2k+1 |
| 3 | 6k+1, 6k+3, 6k+5 | 6k+4, 6k+2 |
| 4 | 12k+2, 12k+4, 12k+8, 12k+10 | 12k+10, 12k+6 |
| 6 | 12k+6, 12k+10 | 12k+4 |
| 16 | 12k+4 | 12k |
| 12 | 12k | - |
Заметим, что после пятого хода Боря мог вычесть из своего числа лишь 2+3+4+6+16=31, т. е. Борино число не могло стать отрицательным. Посмотрим теперь на процесс игры, зная заранее, что достаточно рассматривать остатки при делении Бориного числа на 12 (табл. 2).
| Ход Киры | Возможные остатки от деления на 12 Бориного числа перед её ходом | Возможные остатки от деления на 12 Бориного числа после её хода |
| 2 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 | 11, 1, 3, 5, 7, 9 |
| 3 | 1, 3, 5, 7, 9, 11 | 10, 2, 4, 8 |
| 4 | 2, 4, 8, 10 | 10,6 |
| 6 | 6, 10 | 4 |
| 16 | 4 | 0 |
| 0 | 12k | - |
Таким образом, каждым ходом Кира "отсеивает" некоторые остатки. Уже перед пятым ходом становится ясно, что Борино число имеет вид 12k+4, но приходится назвать "16", чтобы привести его к виду 12k, а уже затем назвать "12".
Примечание. Участниками олимпиады были придуманы и другие последовательности ходов Киры. Среди них особого внимания заслуживает последовательность с минимальной суммой чисел - 6, 4, 3, 2, 5, 12 (попробуйте доказать её минимальность самостоятельно).