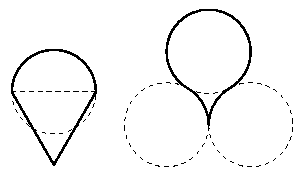
Олимпиада состоялась 2 марта 2003 года, на выполнение задания отводилось 5 астрономических часов.
1. Хулиганы Джей и Боб на уроке черчения нарисовали головастиков (четыре окружности на рисунке - одного радиуса, треугольник - равносторонний, горизонтальная сторона этого треугольника - диаметр окружности). Какой из головастиков имеет бо'льшую площадь?
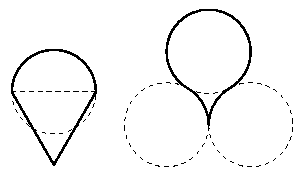
2. Произведение пяти чисел не равно нулю. Каждое из этих чисел уменьшили на единицу, при этом их произведение не изменилось. Приведите пример таких чисел.
3. В магазине три этажа, перемещаться между которыми
можно только на лифте. Исследование посещаемости этажей магазина показало,
что с начала рабочего дня и до закрытия магазина:
1) из покупателей, входящих в лифт на втором этаже, половина едет на
первый этаж, а половина - на третий;
2) среди покупателей, выходящих из лифта, меньше трети делает это на
третьем этаже.
На какой этаж покупатели чаще ездили с первого этажа, на второй или
на третий?
4. Есть шоколадка в форме равностороннего треугольника со стороной n, разделенная бороздками на равносторонние треугольники со стороной 1. Играют двое. За ход можно отломать от шоколадки треугольный кусок вдоль бороздки, съесть его, а остаток передать противнику. Тот, кто получит последний кусок - треугольник со стороной 1, - победитель. Тот, кто не может сделать ход, досрочно проигрывает. Кто выигрывает при правильной игре?
5. В окружность вписан прямоугольный треугольник АВС с гипотенузой АВ. Пусть K - середина дуги ВС, не содержащей точку А; N - середина отрезка АС, М - точка пересечения луча KN с окружностью. В точках А и С проведены касательные к окружности, которые пересекаются в точке Е. Докажите, что /ЕМK = 90o.
6. В тюрьму поместили 100 узников. Надзиратель
сказал им:
"Я дам вам вечер поговорить друг с другом, а потом рассажу
по отдельным камерам, и общаться вы больше не сможете.
Иногда я буду одного из вас отводить в комнату, в которой есть лампа
(вначале она выключена). Уходя из комнаты, вы можете оставить лампу
как включенной, так и выключенной.
Если в какой-то момент кто-то из вас скажет мне, что вы все уже побывали в комнате, и будет прав, то я всех вас выпущу на свободу. А если неправ - скормлю всех крокодилам. И не волнуйтесь, что кого-нибудь забудут - если будете молчать, то все побываете в комнате, и ни для кого никакое посещение комнаты не станет последним."
Придумайте стратегию, гарантирующую узникам освобождение.
1. Ответ: площади фигур равны.
Первое решение. Пусть площадь окружности равна Sокр, а площадь равностороннего треугольника со стороной, равной диаметру окружности, равна Sтр. Так как треугольник O1O2O3 равносторонний, его углы равны 60o, кроме того длина его стороны равна диаметрам исходных окружностей, поэтому его площадь равна Sтр.. Значит, площадь каждого из заштрихованных секторов на рис. 20 равна Sокр/6, а площадь закрашенной части равна
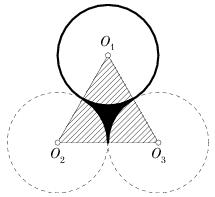 | 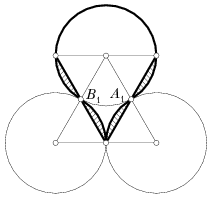 |
| Рис. 20 | Рис. 21 |
Sтр-3(Sокр/6)=Sтр-(Sокр/2)
Поэтому площадь второго головастика равна Sокр+Sтр-(Sокр/2)=Sокр+(Sокр/2). Очевидно, это совпадает с площадью второго головастика.
Идея второго решения. Наложим одного головастика на другого как показано на рис. 21. Нетрудно проверить, что если отрезать от первого головастика заштрихованные сегменты, и повернуть их вокруг точек A1 и B1 на 180o, то получится в точности второй головастик.
2. Ответ: например, 5, 6, 7, 8, -1.
Можно построить и другой пример: пусть первые четыре числа - двойки.
Получаем уравнение на пятое число x:
16x=x-1,
откуда x=-1/15.
3. Ответ: с первого на третий этаж за этот день приехало меньше покупателей, чем с первого на второй.
Первое решение. Предположим, что за весь день на первом этаже в лифт вошло x покупателей, на втором - y, на третьем - z. Заметим, что количество покупателей, вышедших из лифта на каждом из этажей, равно количеству покупателей, вошедших на этом же этаже.
По условию, из покупателей, вошедших на втором этаже, половина едет вниз, а половина - вверх. Значит, со второго этажа на третий едет y/2 покупателей, и столько же со второго на первый. Второе условие можно записать так: z<(x+y+z)/3. Это равносильно тому, что 2z<x+y.
С первого этажа на третий было совершено z-(y/2) поездок, так как всего на третьем этаже вышли из лифта z человек, а y/2 из них приехали со второго этажа. А с первого на второй поднимались те покупатели, входившие в лифт на первом этаже, кто не ехал на третий, т. е. x-(z-(y/2)). Для решения задачи требуется сравнить эти два выражения. Но неравенство z-(y/2)<x-(z-(y/2)) равносильно уже доказанному неравенству 2z<x+y. Тем самым мы доказали, что с первого этажа на третий за этот день приехало меньше покупателей, чем с первого на второй.
Второе решение. Обозначим через n12 количество поездок с первого этажа на второй. Аналогично определим числа n13, n21, n23, n31, n32. Все поездки разобьём на три группы: поездки на третий этаж, поездки с третьего этажа и поездки между первым и вторым этажом. По условию задачи, первая группа составляет менее трети всех поездок. С другой стороны, она количественно равна второй, так как число покупателей, приехавших на третий этаж равно числу уехавших с третьего этажа. Значит, последняя группа составляет более трети всех поездок:
(n31+n32)=(n13+n23)<(n12+n21).
Подставляя в это неравенство n21=n23, получим n13<n12: с первого этажа чаще ездили на второй, нежели на третий.
4. Ответ: если число n является простым, то выигрывает второй игрок, иначе выигрывает первый игрок.
После первого хода образуется равнобедренная трапеция. Посмотрим какие фигуры образуются на последующих ходах.
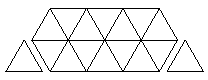 | 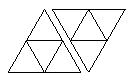 |
| Рис. 22 | Рис. 23 |
Пусть на каком-то ходу один из игроков получил шоколадку в форме равнобедренной трапеции с меньшим основанием a и большим основанием b (длина боковой стороны такой трапеции равна b-a). Если он отломает треугольник, сторона которого меньше, чем b-a, то другой игрок может отломать треугольник со стороной 1, и этот игрок проигрывает (рис. 22}). Следовательно, в этой ситуации он должен отломать треугольник со стороной b-a. После этого хода остаётся параллелограмм, длины сторон которого равны a и b-a.
Пусть игрок получил шоколадку в форме параллелограмма со сторонами a и b, причём a<b. Тогда по аналогичным соображениям он должен отломать треугольник со стороной a. После этого хода остаётся равнобедренная трапеция с основаниями b-a и b.
Таким образом, если в некоторый момент один из игроков получил шоколадку в форме параллелограмма со сторонами a и b (a<b), то через два хода он получит шоколадку в форме параллелограмма со сторонами a и b-a.
Если же один из игроков получил параллелограмм с равными сторонами (т. е. ромб), то после его хода образуется треугольник (рис. 23).
Теперь приведём выигрышную стратегию для второго игрока при простом n. Ему достаточно каждый раз отламывать кусок наибольшего размера. Покажем, что эта стратегия приводит к выигрышу. Пусть первый игрок отломал треугольник со стороной k. После хода второго игрока образуется параллелограмм со сторонами k и (n-k). Эти числа взаимно просты, так как n - простое число. Далее, после каждого хода второго игрока будет получаться параллелограмм (пока в конце концов не получится ромб). Длины сторон этого параллелограмма взаимно просты (если k и n взаимно просты, то k и (n-k) тоже взаимно просты). Значит, длины сторон ромба тоже взаимно просты. Но это означает, что получится ромб со стороной 1 ! Первый будет вынужден отломать от него треугольник со стороной 1, после чего второй выигрывает.
Если n=1, то первый уже выиграл. Пусть теперь число n составное. Обозначим через p любой простой делитель числа n. Пусть первый сначала отломает треугольник со стороной p, а потом каждый раз отламывает самый большой кусок. Через некоторое время второй игрок получит треугольник со стороной p и, как было разобрано выше, через несколько ходов проиграет.
Примечание. Заметим, что описанный процесс есть не что иное, как алгоритм Евклида.
5. Пусть точка O - центр окружности (рис. 24). Так как треугольник ABC прямоугольный, точка O совпадает с серединой гипотенузы AB. Угол NOK прямой: действительно, средняя линия NO треугольника ABC параллельна его стороне BC, а прямая OK является высотой равностороннего треугольника BOC (так как она является биссектрисой этого треугольника).
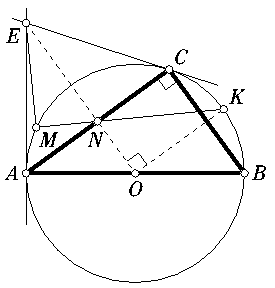
Рис. 24
Нетрудно видеть, что точки E, N и O лежат на одной прямой. Действительно, прямоугольные треугольники ECO и EAO равны по катету и гипотенузе, поэтому EO - биссектриса угла AEC. С другой стороны, треугольник AEC - равнобедренный, так как касательные, проведённые к окружности из одной точки равны. Поскольку отрезок EN - медиана в этом треугольнике, то он также является и биссектрисой. Поэтому лучи EN и EO совпадают как биссектрисы угла AEC.
Точки A, E, C и O лежат на одной окружности, так как /ECO=/EAO=90o. Из теоремы о пересекающихся хордах окружности следует, что
AN*NC=EN*NO. (1)
Применяя ту же теорему к хордам AC и MK исходной окружности, получаем
AN*NC=MN*NK. (2)
Комбинируя (1) и (2), получаем, что
MN*NK=EN*NO.
По теореме, обратной к теореме о пересекающихся хордах получаем, что точки М, K, E и O лежат на одной окружности.
Углы EMK и EOK равны, как опирающиеся на одну дугу. Но угол EOK - прямой, значит, и угол EMK - прямой.
6. Узники выбирают одного определённого человека (будем называть его "счётчиком"), который будет считать узников по такой системе: если, приходя в комнату, он обнаруживает, что свет включён, то он прибавляет к уже посчитанному числу узников единицу и выключает свет, если же свет не горит, то он, ничего не меняя, возвращается обратно в свою камеру. Каждый из оставшихся узников действует по такому правилу: если, приходя в комнату, он обнаруживает, что свет не горит, и он до этого ни разу не включал свет, то он его включает. В остальных случаях он ничего не меняет. Когда число посчитанных узников становится равным 99, "счётчик" говорит, что все узники уже побывали в комнате.
Действительно, каждый узник, кроме "счётчика", включит свет в комнате не более одного раза. Когда "счётчик" насчитает 99, он может быть уверен, что все остальные узники уже побывали в комнате хотя бы раз, кроме того он сам уже побывал в комнате. Получается, что к этому моменту все узники заведомо побывали в комнате хоть раз.
Остаётся доказать, что каждый из 99 узников включит свет. Предположим, что это не так - свет будет включён менее 99 раз. Тогда, начиная с некоторого дня n, свет включаться не будет. Так как никакой заход в комнату не будет для счётчика последним, он побывает в комнате после этого дня (например, на m-й день, m>n). Если свет при этом горел, он его выключит. Значит, начиная с (m+1)-го дня свет будет всё время выключен. Рассмотрим узника, который свет ещё ни разу не зажигал. Так как и для него никакой заход в комнату не последний, он побывает в комнате после m-го дня. Но тогда он должен включить свет - противоречие.