Покажите как по-другому разрезать эту фигуру на две части, из которых тоже можно сложить квадрат.
Олимпиада состоялась 24 февраля 2006 года.
1. В олимпиаде участвовали 2006 школьников. Оказалось, что школьник Вася из всех шести задач решил только одну, а число участников, решивших
2. В клетках таблицы 3x3 расставлены числа так, что сумма чисел в каждом столбце и в каждой строке равна нулю. Какое наименьшее количество чисел, отличных от нуля, может быть в этой таблице, если известно, что оно нечётно?
3. Треугольники ABC и A1B1C1 — равнобедренные прямоугольные (стороны AB и A1B1 — гипотенузы). Известно, что C1 лежит на BC, B1 лежит на AB, а A1 лежит на AC. Докажите, что AA1=2CC1.
4. Девять одинаковых по виду монет расположены по кругу. Пять из них настоящие, а четыре — фальшивые. Никакие две фальшивые монеты не лежат рядом. Настоящие монеты весят одинаково, и фальшивые — одинаково (фальшивая монета тяжелее настоящей). Как за два взвешивания на чашечных весах без гирь определить все фальшивые монеты?
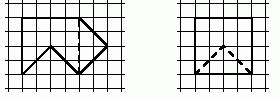
5. Серёжа придумал фигуру, которую легко разрезать на две части и сложить из них квадрат (см. рис.).

Покажите как по-другому разрезать эту фигуру на две части, из
которых тоже можно сложить квадрат.
6.
Каждую неделю Ваня получает ровно одну оценку
(«3», «4» или «5») по каждому
из семи предметов. Он считает неделю удачной, если количество
предметов, по которым оценка улучшилась, превышает хотя бы на два
количество предметов, по которым оценка ухудшилась. Оказалось, что
N недель подряд были удачными, и в последнюю из них оценка
по каждому предмету в точности совпала с оценкой первой недели.
Чему могло равняться число N? (Найдите все варианты.)
1.
Васе на 23 февраля подарили 777 конфет.
Вася хочет съесть
все конфеты за n дней, причем так, чтобы каждый из этих дней
(кроме первого, но включая последний) съедать на одну конфету больше, чем в
предыдущий. Для какого наибольшего числа n это возможно?
2.
На олимпиаде m>1 школьников решали n>1 задач. Все
школьники решили разное количество задач. Все задачи решены разным
количеством школьников. Докажите, что один из школьников решил ровно
одну задачу.
3.
Дан остроугольный треугольник ABC. На сторонах AB и
BC во внешнюю сторону построены равные прямоугольники ABMN и
LBCK так, что AB=KC. Докажите, что прямые AL, NK и MC
пересекаются в одной точке.
4.
В выражении (x4+x3-3x2+x+2)2006
раскрыли скобки и
привели подобные слагаемые. Докажите, что при некоторой степени
переменной x получился отрицательный коэффициент.
5.
Назовем тропинкой замкнутую траекторию на плоскости,
состоящую из дуг окружностей и проходящую через каждую свою точку
ровно один раз. Приведите пример тропинки и такой точки M на
ней, что любая прямая, проходящая через M, делит тропинку
пополам, то есть сумма длин всех кусков тропинки в одной
полуплоскости равна сумме длин всех кусков тропинки в другой
полуплоскости.
6.
Учитель заполнил клетчатую таблицу 5x5 различными целыми числами и
выдал по одной ее копии Боре и Мише. Боря выбирает наибольшее
число в таблице, затем вычеркивает строку и столбец,
содержащие это число, затем выбирает наибольшее число из оставшихся,
вычеркивает строку и столбец, содержащие это число, и т.д. Миша
производит аналогичные операции, каждый раз выбирая наименьшие числа.
Может ли учитель так заполнить таблицу, что сумма пяти чисел, выбранных Мишей,
окажется больше суммы пяти чисел, выбранных Борей?
1.
Один из двух приведенных квадратных трехчленов имеет два
корня меньших тысячи, другой — два корня больших тысячи. Может
ли сумма этих трехчленов иметь один корень меньший тысячи, а
другой — больший тысячи?
2.
Может ли сумма тангенсов углов одного треугольника равняться сумме
тангенсов углов другого, если один из этих треугольников
остроугольный, а другой тупоугольный?
3.
Можно ли замостить всее пространство равными тетраэдрами,
все грани которых — прямоугольные треугольники?
4.
В коробке лежат карточки, занумерованные натуральными
числами от 1 до 2006. На карточке
с номером 2006 лежит
карточка с номером 2005 и т. д. до 1.
За ход разрешается взять
одну верхнюю карточку (из любой коробки) и переложить ее либо на
дно пустой коробки, либо на карточку с номером на единицу больше.
Сколько пустых коробок нужно для того, чтобы переложить все
карточки в другую коробку?
5.
Натуральное число n таково, что 3n+1 и 10n+1 являются
квадратами натуральных чисел. Докажите, что
число 29n+11 — составное.
6.
Дан треугольник ABC и точки P и Q, лежащие на его
описанной окружности. Точку P отразили относительно прямой BC
и получили точку P_a. Точку пересечения прямых QP_a и BC
обозначим A'. Точки B' и C' строятся аналогично. Докажите,
что точки A', B' и C' лежат на одной прямой.
1. Какие значения может принимать
разность возрастающей арифметической
прогрессии a1, a2,..., a5, все члены
которой принадлежат отрезку [0; 3π/2], если числа
cos a1, cos a2, cos a3,
а также числа sin a3, sin a4 и sin a5
в некотором порядке тоже образуют арифметические прогрессии. 2. Найти все несократимые
дроби а/b, представимые в виде b,а
(запятая разделяет десятичные записи натуральных чисел b и а). 3. Можно ли намотать нерастяжимую ленту на бесконечный конус так,
чгобы сделать вокруг его оси бесконечно много оборотов?
Ленту нельзя наматывать на вершину конуса, а также разрезать и перекручивать.
При необходимости можно считать, что она бесконечна, а угол между
осью и образующей конуса достаточно мал.
4. Алиса и Базилио играют в следующую игру; из мешка,
первоначально содержащего 1331 монету, они по очереди берут монеты,
причем первый ход делает Алиса и берет 1 монету, а далее при каждом
следующем ходе игрок берет (по своему усмотрению) либо столько
же монет, сколько взял другой игрок последним ходом,
либо на одну больше. Проигрывает тот, кто не может сделать
очередной ход по правилам. Кто из игроков может обеспечить
себе выигрыш независимо от ходов другого?
5. На биссектрисе данного угла фиксирована точка.
Рассматриваются всевозможные равнобедренные треугольники,
у которых вершина находится в этой точке, а концы оснований лежат
на разных сторонах этого угла. Найти геометрическое место середин
оснований таких треугольников.
6. Все имеющиеся на складе конфеты разных сортов разложены
по n коробкам, на которые установлены цены
в 1, 2, ..., n у.е. соответственно.
Требуется купить такие k из этих коробок наименьшей
суммарной стоимости, которые содержат заведомо
не менее k/n массы всех конфет при одном лишь условии,
что масса конфет в любой коробке не превосходит массы конфет в любой
более дорогой коробке
9 класс
10 класс
11 класс
а) Какие коробки следует купить при n=10 и k=3?
б) Тот же вопрос для произвольных натуральных n ≥ k.
![]()