5 класс | 6 класс | 7 класс | 8 класс | 9 класс | 10 класс | 11 класс
архив этой страницы вместе с картинками: okrm2001.zip (36886)
1. В числе 3728954106 зачеркните три цифры так, чтобы оставшиеся цифры в том же порядке составили как можно меньшее число.
Ответ: 2854106. Рассуждения, приводящие к верному ответу, школьник может не записывать.
2. Кузнечик прыгает по прямой вперед и назад большими и малыми прыжками. Большой прыжок составляет 12 см, малый - 7 см. Покажите, как ему попасть из точки А в точку В, если расстояние между этими точками 3 см.
Сначала кузнечик делает два больших прыжка из точки А в направлении точки В, а затем делает три малых прыжка в обратном направлении, так как 2*12 - 3*7 = 3. Возможны решения и с большим количеством прыжков.
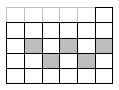
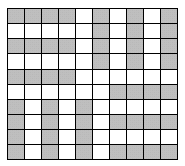
3. Разрежьте фигуру (см. рис.) на 5 частей одинаковой формы и одинакового размера так, чтобы в каждую часть попало ровно по одному серому квадратику.

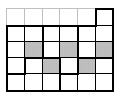
Решение.
4. При сложении двух натуральных чисел Коля поставил лишний ноль на конце первого слагаемого и вместо 2801 получил сумму, равную 10001. Какие числа складывал Коля?
Если к десятичной записи натурального числа приписать ноль в конце, то оно увеличится в десять раз, то есть, сумма увеличится на девять первых слагаемых. Значит, первое слагаемое равно: (10001 - 2801) : 9 = 800. Второе слагаемое равно: 2801 - 800 = 2001. (Если а + b = 2801 и 10а + b = 10001, то 9а = 10001 - 2801; 9а = 7200; а = 800; b = 2001.)
Ответ: 800 и 2001.
5. В хороводе по кругу стоят 15 детей. Справа от каждой девочки стоит мальчик. У половины мальчиков правый сосед тоже мальчик, а у каждого из остальных мальчиков правый сосед - девочка. Сколько мальчиков и сколько девочек в хороводе?
Так как у каждой девочки правый сосед - мальчик, то в хороводе должны быть пары Д - М (слева направо: девочка - мальчик). Хоровод не может состоять только из таких пар, потому что у половины мальчиков соседи справа - мальчики. Значит, в хороводе должны быть "тройки" Д - М - М. У другой половины мальчиков правые соседи - девочки, значит, должно быть: Д - М - М - Д - ... . Таким образом, хоровод состоит из пяти "троек" вида Д - М - М, то есть, мальчиков в два раза больше, чем девочек.
Ответ: девочек - 5; мальчиков - 10. Ответ можно также дать в виде рисунка.
1. Вася решал пример на черновике, а затем переписал решение в
тетрадь, но забыл поставить скобки. Вот, что у него получилось:
6 * 8 + 20 : 4 - 2 = 40. Расставьте забытые Васей скобки.
Ответ: 6 * (8 + 20) : 4 - 2 = 40.
2. Художник Худобеднов за месяц работы написал 42 картины. На 17 из них есть лес, на 29 - река, а на 13 - и то, и другое. На остальных картинах - не пойми что. Сколько картин изображают не пойми что?
Количество картин, на которых есть хотя бы что-то равно: (29 + 17) - 13 = 33. Следовательно, не пойми что изображают 42 - 33 = 9 картин. Решение можно пояснить на диаграмме (круги Эйлера).
Ответ: 9.
3. В корзине лежат 13 яблок. Имеются весы, с помощью которых можно узнать суммарный вес любых двух яблок. Придумайте способ выяснить за 8 взвешиваний суммарный вес всех яблок.
Взвесим яблоки парами, например, первое и второе, третье и четвертое, ..., одиннадцатое и двенадцатое. Это - 6 взвешиваний. Седьмое взвешивание - одиннадцатое и тринадцатое яблоко; восьмое - двенадцатое и тринадцатое. Тогда, сложив результаты трех последних взвешиваний, получим удвоенный вес яблок N 11, N 12 и N 13, и, значит, сумеем вычислить и суммарный вес всех яблок.
4. В городе Пряничном мэр задумал ввести налог на пряники - каждый, кто покупает пряник, должен заплатить 20% от стоимости пряника в городскую казну. А заместитель же мэра предложил поднять цену на пряники на 20%, и забирать в казну 20% выручки продавцов. Какое из двух предложений (мэра или его заместителя) принесет в казну больше денег?
Пусть стоимость пряника - x рублей. Тогда, в первом случае, казна получит с каждого пряника 0,2x рублей, а во втором случае - 1,2х*0,2 = 0,24x рублей.
Ответ: больше денег принесет в казну предложение заместителя мэра.
5. Покажите, как разрезать данную фигуру (см. рис.) на четыре одинаковые части и сложить из них квадрат 6*6 с шахматной раскраской.
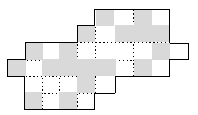
Заметим, что между клетками одного цвета должен обязательно пройти разрез, и получим ответ (см. рис.):
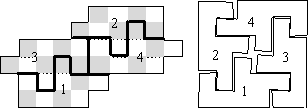
1. Придумайте дробь, которая больше, чем 9/10, но меньше, чем 10/11. Ответ поясните.
Приведем к общему знаменателю: 9/10 = 99/110; 10/11 = 100/110. Умножим числители и знаменатели полученных дробей на какое-либо натуральное число, например, на 2. Получим дроби: 198/220 и 200/220. Искомой дробью является, например, 199/220. К такому же ответу приводит рассуждение о том, что полусумма двух положительных чисел "находится между ними".
Другой возможный способ решения связан с переводом данных дробей в десятичные: 9/10 = 0,9; 10/11 = 0,9090... , тогда, искомой дробью является, например, 0,905.
2. В треугольнике АВС проведена медиана ВD. Точки E и F делят медиану на три равных отрезка (BE = EF = FD). Известно, что AB = 1 и AF = AD. Найдите длину отрезка CE.
Докажем, что треугольники ABF и CЕD равны (см. рис.).
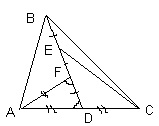
Заметим, что AF = DC и BF = ED.
Так как AFD - равнобедренный треугольник,
то /AFD = /ADF. Углы, смежные с ними, также равны:
/AFB = /EDC. Следовательно,
DABF = DCЕD
по двум сторонам и углу между ними, значит, CE = AB.
Ответ: СЕ = 1.
3. В школе прошли три олимпиады. Оказалось, что в каждой из них участвовало по 50 человек. Причем, 60 человек приходило только на одну олимпиаду, а 30 человек - ровно на две. Сколько человек приняло участие во всех трех олимпиадах?
Пусть х человек приняло участие во всех трех олимпиадах. Подсчитаем, сколько раз ученики заполняли титульные листы своих работ. Те, кто приходили один раз, делали это 60 раз; те, кто приходили дважды - также 60 раз (2*30 = 60); те, кто приходили трижды - 3х раз. Так как всего работ было 3*50 = 150, то составляем и решаем уравнение: 60 + 60 + 3x = 150; x = 10.
Ответ: 10.
4. "Жигули" и "Москвич" одновременно подъехали к бензоколонке, находящейся в 40 км по шоссе от поста ГАИ. "Москвич" проехал мимо этого поста на полчаса позже "Жигулей". С какой скоростью ехал "Москвич", если скорость "Жигулей" - 80 км/ч?
Выясним, в каком направлении ехала каждая машина. Предположим, что "Жигули" ехала в направлении от поста ГАИ к бензоколонке. Так как расстояние между ними - 40 км, а скорость "Жигулей" - 80 км/ч, то "Жигули" затратили на этот путь 0,5 часа. Но, в этот момент, согласно условию, "Москвич" должен проезжать пост ГАИ, поэтому у бензоколонки находиться не может. Значит, "Жигули" ехало в противоположном направлении. "Москвич" ехал в том же направлении, что и "Жигули", поскольку проезжал пост ГАИ на полчаса позже, значит, на путь в 40 км он затратил 1 час, то есть, его скорость - 40 км/ч.
Ответ: 40 км/ч.
5. У Вани работает 10 сотрудников. Каждый месяц Ваня повышает зарплату на 1 рубль ровно девятерым (по своему выбору). Как Ване повышать зарплаты, чтобы сделать их одинаковыми? (Зарплата - целое число рублей.)
Тот, кому не добавили рубль, относительно других сотрудников этот рубль теряет. Не будем доплачивать сотруднику с самой большой зарплатой до тех пор, пока его зарплата не сравняется с той, которая была самой маленькой (если сотрудников с наибольшей зарплатой - несколько, то выберем любого из них). Таким образом, наименьшую зарплату будут иметь, по крайней мере, двое сотрудников. Затем, снова выберем сотрудника с самой большой зарплатой и не будем ему доплачивать, пока его зарплата не сравняется с той, которая была самой маленькой, и получим не менее трех сотрудников с одинаковой зарплатой. Проделав такую операцию не более девяти раз, Ваня сможет уравнять все зарплаты.
1. Сократите дробь (9+a)/(3+(-a)1/2)
Пусть b = (-a)1/2, тогда,
а = -b2. Подставим в данное выражение, разложим
числитель на множители и сократим:
(9-b2)/(3+b) =
(3-b)(3+b)/(3+b) = 3-b
Аналогичные операции можно проделать и без замены переменной, но учитывая,
что a<0.
Ответ: 3-(-a)1/2
2. Два торговца купили в городе одинаковое количество товара по одной и той же цене и увезли каждый в свою деревню продавать. Первый продавал товар в два раза дороже закупочной цены. Второй сначала поднял цену на 60%, продал четвертую часть товара, затем поднял цену еще на 40% и продал остальное. Кто из них выручил больше денег?
Пусть стоимость всего купленного товара - x рублей, тогда, первый торговец продал весь товар за 2x рублей. Второй - сначала продал четверть товара, подняв цену на 60%, то есть, получил за это 1,6*0,25x рублей. Затем продал остальное, подняв новую цену еще на 40%, то есть получил 1,6*1,4*0,75x рублей. Получается, что второй продал весь товар за 1,6*0,25x + 1,6*1,4*0,75x = 0,4x + 1,68x = 2,04x(рублей). Это больше, чем 2x, значит, второй выручил больше денег.
Ответ: второй торговец.
3. Дана трапеция АВСD (ВС || DA). Через середину М боковой стороны АВ проведена прямая, параллельная основаниям. Биссектриса угла АВС пересекает эту прямую в точке О. Докажите, что АО - биссектриса угла BАD.
Пусть K - точка пересечения BK и AD (см. рис.).
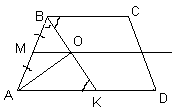
Так как /AKB = /CBK = /ABK, то
DABK - равнобедренный
(AB = AK). O - середина BK (по теореме Фалеса),
значит, АО - медиана DABK, которая
одновременно является и биссектрисой. Следовательно, АО - биссектриса
угла BАD, ч. т. д. Суть приведенного решения не изменится, если
AD будет меньшим основанием трапеции. Также возможны схожие
рассуждения, связанные с доказательством равнобедренности треугольников
BМО и АМО.
4. Может ли число, сумма цифр которого равна 2001, быть квадратом целого числа?
Ответ: не может. Предположим, что это не так, и заметим, что данное число делится на 3, но не делится на 9 (признаки делимости). Но, если произвольное натуральное число n разложить на простые множители, то в аналогичное разложение числа n2 эти множители войдут с четными показателями степеней. Значит, если квадрат целого числа делится на 3, то он делится и на 9. Получено противоречие, следовательно данное число не является квадратом никакого целого числа.
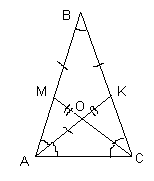
5. Треугольник АВС равнобедренный: АВ = ВС = 1, /ABC = 36o. Биссектрисы АK и СM пересекаются в точке О. Найдите периметр треугольника АМО.
Так как треугольник АВС - равнобедренный и
/ABC = 36o, то
/BАC = /BСA = 72o (см. рис.).
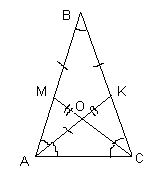
Так как АK и СM - биссектрисы треугольника, то
/ВАK = /CAK = /BCM =
/ACM = 36o.
/AВK = /BAK, значит,
DАВК - равнобедренный
(АК = ВК).
DАМС =
DСКА (по II признаку равенства
треугольников), значит, АК = СM и СK = АМ, тогда,
ВМ = ВК.
DАОС - равнобедренный, значит,
АО = ОС, так как АК = МС, то МО = ОК.
РDАМО = АО + ОМ + АМ = АО + ОК + АМ = AK + AM = ВK + АМ = ВМ + АМ = АВ = 1.
Ответ: 1.
6. Из трех мальчиков, которых зовут Антон, Ваня и Саша, только один всегда говорит правду. Антон сказал: "Ваня не всегда говорит правду", Ваня сказал: "Я не всегда говорю правду", а Саша сказал: "Антон не всегда говорит правду". Кто же из них всегда говорит правду, если известно, что по крайней мере один из них солгал?
1) Легко видеть, что Ваня говорит правду (если предположить, что он лжет и
высказывание "Я не всегда говорю правду" - не является правдой, то правдой
будет: "Я всегда говорю правду", то есть, получится противоречие).
2) Так как смысл высказывания Антона такой же, то Антон тоже говорит
правду.
3) По условию, один из мальчиков солгал, значит, это - Саша.
4) Саша сказал: "Антон не всегда говорит правду" - и при этом солгал,
значит, Антон всегда говорит правду.
Ответ: Антон.
1. Решите систему уравнений:
| { | xy = 1; |
| yz = 2; | |
| zx = 8. |
Перемножим уравнения почленно, тогда, (xyz)2 = 16 => xyz = +4. Следовательно, z = +4; x = +2; y = +0,5. Учитывая, что числа x, y и z - одного знака, получаем ответ: (2; 0,5; 4); (-2; -0,5; -4). Возможны также решения и способом подстановки.
2. На гипотенузе AB прямоугольного треугольника ABC во внешнюю сторону построен квадрат со стороной AB. Точка D - центр этого квадрата. Найдите величину угла ACD.
Рассмотрим окружность, описанную около прямоугольного треугольника
ABC (см. рис.).
Отрезок AB является диаметром этой окружности. Так как
/ADВ = 90o, то точка D лежит на этой
окружности. По теореме об углах, вписанных в окружность,
/ACD = /ABD = 45o.
3. Можно ли в квадрате 10*10 расставить 12 кораблей размером 1*4 (для игры типа "морской бой") так, чтобы корабли не соприкасались друг с другом (даже вершинами)?
Ответ: можно (см. рис.).
4. Докажите, что если a, b, c - нечётные числа, то хотя бы одно из чисел ab- 1, bc - 1 или ac - 1 делится на 4.
Остаток от деления нечетного числа на 4 может быть либо 3, либо 1. Если среди чисел a, b, c есть хотя бы два числа, остатки от деления которых на 4 равны 1, то их произведение при делении на 4 также даёт остаток 1. Следовательно, разность этого произведения и единицы делится на 4, ч. т. д.
В противном случае, среди данных найдутся хотя бы два числа, остатки от деления которых на 4 равны 3. Так как (4m + 3)*(4n+ 3) - 1 = 16mn + 12m+ 12n + 8 = 4(4mn + 3m + 3n + 2), то разность произведения этих чисел и единицы делится на 4, ч. т. д.
5. Точки M и N лежат, соответственно, на сторонах BC и CD параллелограмма ABCD, причём BM:MC = 1:3 и CN:ND = 2:5. Отрезки AN и DM пересекаются в точке K. Найдите отношение AK:KN.
Первый способ. Проведем через точки B и C прямые,
параллельные прямой DM (см. рис.).
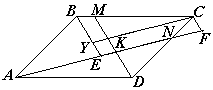
Обозначим точки пересечения этих прямых с прямой AN соответственно
Е и F. Так как треугольники CNF и DNK - подобны,
то FN:NK = CN:ND = 2:5, тогда,
FN=(2/5)NK. По теореме о пропорциональных отрезках,
EK:KF = BM:MC = 1/3, тогда,
EK = (1/3)KF = (1/3)(KN+NF) =
(1/3)(KN+(2/5)KN) = (7/15)KN.
Проведем CY||AN, тогда, треугольники CYB и AKD
равны, следовательно, AK = CY. Так как CFEY -
параллелограмм, то EF=CY=AK.
Поэтому, AK:KN=EF:KN =
(EK+KN+NF):KN =
((7/15)KN+KN+(2/5)KN):KN = 28:15.
Второй способ. [В этом абзаце жирным шрифтом обозначены
вектора, обычным - числа.]
Пусть AB=x, AD=y.
Тогда AN=(5/7)x и
DM=x-(3/4)y.
Так как DK||DM, то существует k, такое что
DK = kDM =
kx-(3/4)ky .
AK = AD+DK =
kx+(1-(3/4)k)y .
DM = x-(3/4)y.
Так как
AK||AN, то существует n,
такое что
AK = nAN.
Получаем векторное уравнение:
kx+(1-(3/4)k)y =
(5/7)nx+ny
Учитывая, что x и x - не коллинеарны, получаем
систему уравнений:
| { | k=(5/7)n | => | { | k=20/43 |
| 1-(3/4)k=n | n=28/43 |
6. а) Докажите, что существует квадрат, все вершины и все середины сторон которого лежат на гиперболах y=+(1/x).
б) Найдите площадь такого квадрата.
а) Пусть точка A(a; 1/a) лежит на гиперболе
y=1/x в первой координатной четверти (а>0).
Рассмотрим поворот с центром в начале координат на угол 90o
по часовой стрелке (см. рис.).
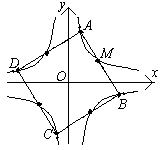
Получим точку В(1/a; -a), принадлежащую гиперболе
y=-1/x. Середина отрезка АВ имеет координаты:
M((a2+1)/(2a);
(1-a2)/(2a)). Выясним, существуют ли значения а
такие, что точка М лежит на первой гиперболе. Составим уравнение:
((a2+1)/(2a))*((1-a2)/(2a)) = 1,
которое имеет единственный положительный корень
a=(51/2-2)1/2. При рассмотренном повороте точка
B перейдет в точку С, С - в D, D -
в А. Так как при таком повороте ветви гипербол переходят друг в друга,
то эти точки лежат на гиперболах. Четырехугольник ABCD - квадрат
(свойства поворота на 90o). Середины его сторон при указанном
повороте переходят друг в друга и лежат на гиперболах, ч. т. д.
б) Площадь квадрата равна квадрату его стороны. Используя формулу расстояния между точками на координатной плоскости, получим: АВ2 = 2(a2+(1/a2)) = 4*51/2.
1. Определите количество корней уравнения sin px * tg px = tg px, принадлежащих промежутку [0; 2000].
Данное уравнение равносильно совокупности
| [ | tg px = 0 | (А) | |
| { | sin px = 1 | (Б) | |
| cos px не равно 0 | |||
Ответ: 2001.
2. Ежедневно в полдень из Москвы в Астрахань и из Астрахани в Москву выходит рейсовый теплоход. Теплоход, вышедший из Москвы, идет до Астрахани ровно четверо суток, затем двое суток стоит, и в полдень, через двое суток после своего прибытия в Астрахань, отправляется в Москву. Теплоход, вышедший из Астрахани, идет до Москвы ровно пять суток и, после двухсуточного отдыха в Москве, отправляется в Астрахань. Какое наименьшее количество теплоходов должно работать на линии Москва - Астрахань - Москва при описанных условиях движения?
Рассмотрим ситуацию в полночь: по маршруту Москва - Астрахань движутся 4 теплохода (первому осталось 3,5 суток до прибытия в Астрахань, а четвертому - 0,5 суток). По маршруту Астрахань - Москва движутся 5 теплоходов, в Москве, как минимум, 2 теплохода, и в Астрахани также, как минимум, 2 теплохода. Итого: 4 + 5 + 2 + 2 = 13 теплоходов.
Ответ: 13.
3. Отрезки ОА, ОВ и ОС - попарно взаимно перпендикулярны. Могут ли стороны треугольника АВС относиться, как 3:4:6 ?
Пусть в треугольнике АВС: АВ = 3k, BC = 4k, AC = 6k. Обозначив данные отрезки a, b и c соответственно, по теореме Пифагора получаем систему уравнений:
| { | a2+b2=9k2 |
| b2+c2=16k2 | |
| a2+c2=32k2 |
Ответ: не могут.
4. Пусть а1, а2, а3, ... а2001 - некоторые целые числа. b1, b2, b3, ... b2001 - те же числа, записанные в другом порядке. Докажите, что произведение (a1-b1)*(a2-b2)*(a3-b3)*...*(a2001-b2001) является четным числом.
Каждый из множителей - целое число. Предположим, что произведение не является четным числом, тогда все множители должны быть нечетными. Так как количество множителей также нечетно, то их сумма должна быть нечетным числом, но эта сумма, очевидно, равна нулю. Полученное противоречие доказывает ошибочность предположения, то есть, данное произведение является четным числом, ч. т. д.
5. После того, как Левша подковал блоху, блоха совершает каждый следующий прыжок вдвое короче предыдущего: если первый прыжок был длиной в аршин, то второй - в пол-аршина, третий - в четверть аршина и т. д. Сможет ли блоха побывать в какой-нибудь точке плоскости дважды?
Пусть блоха попала в какую-то точку. Рассмотрим дальнейшие ее прыжки. Их
длины составляют геометрическую прогрессию со знаменателем 0,5. Рассмотрим
сумму этой прогрессии. Используя формулу
Sn =
b1(qn-1)/(q-1),
получим:
Sn =
b1(2-(1/2n-1)) =
2b1-(b1/2n-1).
Sn-b1 =
b1 - (b1/2n-1) <
b1, то есть длина первого прыжка больше суммы всех
остальных. Ломаная, у которой длина одного звена больше суммы длин остальных
звеньев, не может быть замкнутой, следовательно, вернуться в исходную точку
блоха не сможет.
Ответ: нет.
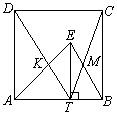
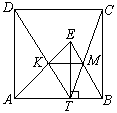
6. Внутри квадрата ABCD взята точка Е. ET - высота треугольника АВЕ, К - точка пересечения прямых DT и AE, М - точка пересечения прямых СТ и ВЕ. Докажите, что отрезок КМ является стороной квадрата, вписанного в треугольник АВЕ.
Пусть, ЕТ = h, а сторона квадрата равна а. Из подобия
треугольников ADK и ETK (см. рис. 1) следует, что
AK/EK=DK/TK=a/h.
Аналогично, из подобия треугольников BCM и ETM следует, что
BM/EM=a/h.
Из равенства AK/EK=DK/TK=BM/EM=a/h
следует, что
AE/KE=DT/KT=BE/ME=(a+h)/h.
Так как Е - общий угол треугольников АЕВ и КЕМ и
AE/KE=BE/ME=(a+h)/h,
то DАЕВ подобен
DКЕМ. Из подобия этих треугольников следует
что AB/KM=(a+h)/h и равенство углов
ВАЕ и МКЕ. Следовательно, отрезки КМ и АВ
параллельны (см. рис. 2), причем
KM=ah/(a+h).
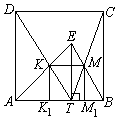
Проведя КК1 и ММ1 - перпендикуляры к
АВ (см. рис. 3), получим прямоугольник
КК1М1М, вписанный в треугольник
АВЕ. Из подобия треугольников DAT и KK1T
следует, что DA/KK1=DT/KT,
то есть KK1=ah/(a+h)=KM.
Следовательно, КК1М1М - квадрат,
ч. т. д.
 |  |  |
| Рис. 1. | Рис. 2. | Рис. 3. |
1. Докажите, что уравнение x2000+3x2-31/2x+1=0 не имеет действительных корней.
Так как квадратное уравнение 3x2-31/2x+1=0 не имеет действительных корней (D<0), а "ветви" соответствующего квадратного трехчлена направлены вверх, то для любого x верно неравенство 3x2-31/2x+1>0. Следовательно, для любого x верно и неравенство x2000+3x2-31/2x+1>0, то есть данное уравнение не имеет действительных корней, ч. т. д.
2. На рисунке изображен график функции
f(x)=x4-x2+bx+c.
Определите знаки коэффициентов b и c.
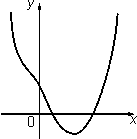
Ответ: b<0; c>0.
Заметим, что f(0)=c>0. Найдем производную данной функции: f'(x)=4x3-2x+b. Тогда f'(x)=b<0;, так как данная функция в точке x=0 убывает.
3. Докажите неравенство: (ab+bc+ca)/2<c2, если a и b - катеты прямоугольного треугольника, а c - его гипотенуза.
Данное неравенство равносильно неравенству:
ab+bc+ca<2c2,
которое, в свою очередь, равносильно неравенству
ab+bc+ca<a2+b2+c2
(теорема Пифагора). Для доказательства последнего неравенства рассмотрим и
преобразуем разность между его правой и левой частью:
a2+b2+c2-ab-bc-ca =
= (1/2)(2a2+2b2+2c2-2ab-2bc-2ca) =
= (1/2)((a-b)2+(b-c)2+(c-a)2)>0.
Так как a, b и c - стороны прямоугольного треугольника
(который не может быть равносторонним), то последнее неравенство - строгое.
Таким образом, выполняется и исходное неравенство, ч. т. д.
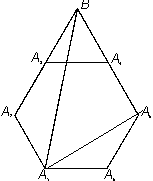
4. На листе бумаги нарисован правильный шестиугольник со стороной 1. Используя только линейку без делений постройте отрезок длины 71/2.
Пусть А1А2...А6 - данный правильный шестиугольник. Продолжив его стороны А2А3 и А5А4 до пересечения в точке В, получим искомый отрезок A1B (см. рис.).
Доказать, что этот отрезок равен 71/2, можно различными
способами. Например, из того, что
DА3А4В -
равносторонний следует, что
А2В=А5В=2. Далее, либо
применяем теорему косинусов для треугольника
А1А2В со сторонами 1 и 2 и углом
120o, либо из треугольника
А1А5А6 по теореме
косинусов находим, что
А1А5=31/2, а затем, применяем
теорему Пифагора для треугольника
А1А5В
(/А1А5В=90o).
5. Решите систему уравнений:
| { | 2y - x = sin x - sin 2y |
| cos x + 5 sin y = 4 |
Приведем первое уравнение к виду
2y + sin 2y = x + sin x и рассмотрим функцию
f(t) = t + sin t.
Так как f'(t) = 1 + cos t то эта функция - возрастает
(в данном случае для этого достаточно нестрогого неравенства, так как график
функции не содержит отрезков, параллельных оси x). Возрастающая
функция принимает каждое свое значение ровно один раз, следовательно,
x=2y. Решая уравнение
cos 2y + 5 sin y = 4, получим:
1 - 2 sin2 y + 5 sin y = 4 =>
2 sin2 y - 5 sin y + 3 = 0 =>
sin y = 1 =>
y=(p/2)+pn.
Ответ:
x=p+2pn,
y=(p/2)+pn.
nCZ.
6. Можно ли расположить в пространстве 8 непересекающихся треугольных пирамид так, чтобы любые две из них соприкасались частью своей поверхности?
Ответ: Можно.
Например: ABC - основание тетраэдра SABC, разбитое на части, как показано на рис. 1, A1B1C1 - основание тетраэдра S1A1B1C1, разбитое на части, как показано на рис. 2. Тетраэдры зеркально симметричны и соединены основаниями, как показано на рис. 3.
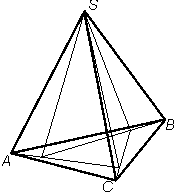 | 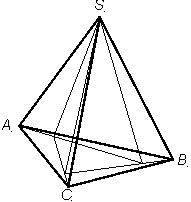 | 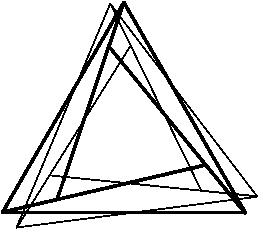 |
| Рис. 1. | Рис. 2. | Рис. 3. |