1. Тангенсы углов треугольника - натуральные числа.
Чему они могут быть равны.
(А. Заславский)
Ответ: тангенсы углов треугольника равны 1, 2 и 3.
Решение 1. Обозначим углы треугольника (в порядке неубывания) через a, b, g. Тогда 0<a<p/3, поэтому 0<tg a<31/2. Так как tg a - натуральное число, то он равен 1, a=p/4. Тогда b+g=3p/4, откуда
-1=tg(b+g) = (tg b + tg g)/(1 - tgb tg g) ,
tg b + tg g = tg b tg g - 1 ,
(tg b - 1)(tg g - 1) = 2.
Число 2 - простое, поэтому одна скобка равна 1, а другая 2. Отсюда получаем: tg b = 2, tg g = 3.
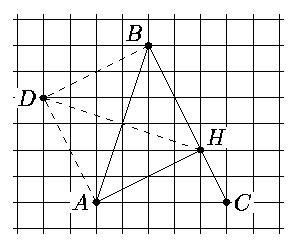
Решение 2. Нарисуем на клетчатой бумаге треугольник ABC, как
показано на рисунке. Подсчётом клеточек легко убедиться, что
tg /BAC=3, tg /ACB=2. Отметим теперь точки
H и D. Опять-таки из подсчёта клеточек следует, что ADBH -
ромб с равными диагоналями, то есть квадрат.
Поэтому /ABC=p/4,
а tg /ABC=1. Итак, нарисованный треугольник удовлетворяет условию.

Покажем, что других значений тангенсов быть не может. Как было доказано в решении 1, наименьший из углов треугольника обязательно равен p/4. При этом остальные углы строго больше: если бы второй угол также равнялся p/4, то третий угол был бы равен p-(2p/4)=p/2 и его тангенс был бы не определён. Таким образом, один из тангенсов равен 1, а два остальных - больше 1.
Поскольку сумма углов треугольника равна p, нельзя изменить значение тангенса одного угла, не меняя значений остальных двух. Значит, кроме варианта 1, 2, 3 осталось рассмотреть случай, когда один из тангенсов равен 1, а два других - больше 3. В этом случае пришлось бы увеличить два угла треугольника ABC, оставив третий без изменений, что невозможно по той же теореме о сумме углов треугольника. Итак, вариант на рисунке - единственный.
2. Про положительные числа a, b, c известно,
что (1/a)+(1/b)+(1/c)>a+b+c.
Докажите, что a+b+c>3abc.
(С. Злобин)
Решение. Умножая неравенство (1/a)+(1/b)+(1/c)>a+b+c на общий знаменатель, получаем равносильное неравенство bc+ac+ab>(a+b+c)abc.
Теперь докажем вспомогательное неравенство
(a+b+c)2>3(ab+bc+ca) :
(a-b)2+(b-c)2+(c-a)2>0 <=>
<=> 2(a2+b2+c2)>2(ab+bc+ca) <=>
<=> a2+b2+c2>ab+bc+ca <=>
<=> a2+b2+c2+2(ab+bc+ca)>3(ab+bc+ca) <=>
<=> (a+b+c)2>3(ab+bc+ca).
Отсюда легко получить требуемое неравенство:
(a+b+c)2>3(ab+bc+ca)>3(a+b+c)abc,
a+b+c>3abc.
3. В выпуклом четырёхугольнике ABCD точки E и F
являются серединами сторон BC и CD соответственно.
Отрезки AE, AF, BF делят четырёхугольник
на 4 треугольника, площади которых равны последовательным натуральным числам.
Каково наибольшее значение площади треугольника ABD?
(С. Шестаков)
Ответ: 6.
Решение. Пусть площади треугольников равны
n, n+1, n+2, n+3. Тогда площадь четырёхугольника
ABCD составляет 4n+6. Площадь треугольника BCD равна
учетверённой площади треугольника ECF. Значит,
SABD=SABCD-SBCD<(4n+6)-4n=6.
Равенство достигается, если треугольник ECF имеет наименьшую
площадь из указанных четырёх треугольников.
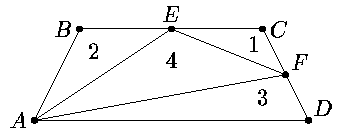
Осталось доказать, что значение 6 является возможным. Примером служит равнобедренная трапеция с основаниями AD=6, BC=4 и высотой 2 (числа на рисунке обозначают площади треугольников).
4. Каждый зритель, купивший билет в первый ряд
кинотеатра, занял одно из мест в первом ряду. Оказалось, что все места в
первом ряду заняты, но каждый зритель сидит не на своём месте. Билетёр может
менять местами соседей, если оба сидят не на своих местах. Всегда ли он может
рассадить всех на свои места?
(А. Шаповалов)
Ответ: всегда.
Решение. Занумеруем всех зрителей номерами их билетов 1, ..., n. Пусть, для определённости, самое правое место имеет номер n, а самое левое - номер 1. Будем решать задачу индукцией по количеству зрителей. Мы сведём задачу к той же задаче с меньшим числом зрителей, пересадив зрителя n на своё место.
Пусть билетёр действует следующим образом. Он пересаживает зрителя n вправо, если его правый сосед при этом не садится на своё место. Если зрителя n не удаётся пересадить правее с места k, то на (k+1)-м месте сидит зритель k. Выберем наибольшее m такое, что зрители с номерами k, k+1, ..., k+m-1 сидят на местах k+1, k+2, ..., k+m соответственно. Возможны два случая: k+m<n или k+m=n.
В первом случае на (k+m+1)-м месте сидит зритель j, j не равно k+m. Поэтому безопасно пересадить j налево, потом ещё раз налево и т. д., пока он не поменяется местами со зрителем n. В результате билетёру удастся пересадить зрителя n на одно место правее, и он может повторять эту процедуру до тех пор, пока не произойдёт одно из двух: зритель n окажется на своём месте или встретится второй случай.
Во втором случае билетёр может рассадить по своим местам зрителей k, k+1, ..., n, пересаживая зрителя n вправо до его места.
Таким образом, несколько зрителей в правом конце ряда будут сидеть на своих местах, а остальные - нет. Задача сведена к исходной с меньшим числом зрителей.
5.
В городе Удоеве выборы мэра проходят следующим образом. Если
в очередном туре голосования никто из кандидатов не набрал больше половины
голосов, то проводится следующий тур с участием всех кандидатов, кроме
последнего по числу голосов. (Никогда два кандидата не набирают голосов
поровну; если кандидат набрал больше половины голосов, то он становится
мэром и выборы заканчиваются.) Каждый избиратель в каждом туре голосует
за одного из кандидатов. Если это кандидат вышел в следующий тур, то
избиратель снова голосует за него. Если же кандидат выбыл, то все его
избиратели голосуют за одного и того же кандидата из числа оставшихся.
На очередных выборах баллотировалось 2002 кандидата. Мэром стал
Остап Бендер, занявший в первом туре k-е место по числу голосов.
Определите наибольшее возможное значение k, если Остап Бендер
был избран
а) в 1002-м туре;
б) в 1001-м туре.
(Б. Френкин)
Ответ:
а) k=2001;
б) k=1.
Решение. а) Остап не мог занять последнее, 2002-е место в первом туре, поскольку иначе он сразу же выбыл бы из числа кандидатов. Поэтому k<2001.
Пусть все кандидаты в первом туре набрали почти поровну, Остап занял предпоследнее место и в каждом следующем туре получал все голоса выбывшего кандидата. Тогда Остап победит в тот момент, когда количество выбывших кандидатов достигнет половины. Это случится как раз в 1002-м туре.
Выполним точный подсчёт в случае, когда кандидаты в первом туре набрали
106, 106+1, ..., 106+2001 голос. Тогда в
1001-м туре у Остапа ещё меньше половины голосов, а именно: голоса всех
кандидатов, занявших последние 1001 место в первом туре. Однако в 1002-м туре
у него уже более половины всех голосов. Действительно, у Остапа
106+(106+1)+...+(106+1001)=
=1002*106+(1001*1002)/2=
=1002*106+1001*501=1002501501
голосов, а всего избирателей
106+(106+1)+...+(106+2001)=
=2002*106+(2001*2002)/2=
=2002*106+2001*1001=2004003001.
Нетрудно проверить, что это меньше удвоенного числа голосов Остапа.
б) Предположим, что k>1. Кандидата, занявшего первое место в первом туре, назовём фаворитом. Тех, кто выбыл в первой тысяче туров, назовём аутсайдерами, а всех остальных кандидатов, кроме Остапа, - лидерами. Поскольку число аутсайдеров 1000, а лидеров 1001, то один из лидеров не получал голосов аутсайдеров. В первом туре (и позже) он имел больше голосов, чем любой аутсайдер (так как в конечном счёте выбыл аутсайдер, а не этот лидер). Поэтому фаворит, набравший в первом туре наибольшее число голосов, не входит в число аутсайдеров.
Максимальное число голосов, которое мог собрать Остап к 1001-му туру, - это все голоса аутсайдеров на момент вылета каждого из них и голоса первоначальных избирателей Остапа. Любой из лидеров в любом из первой тысячи туров (а тем более в 1001-м) имеет больше голосов, чем аутсайдер этого тура. Фаворит заведомо имеет больше, чем имел Остап в первом туре. Поэтому лидеры в сумме имеют в 1001-м туре больше голосов, чем Остап, и он не может стать победителем.
Дополнительный вопрос (в условие предлагавшейся на олимпиаде задачи не входит): изменится ли ответ в задаче, если голоса выбывшего кандидата произвольно делятся между оставшимися?
6. Можно ли раскрасить все точки квадрата и круга в чёрный и
белый цвета так, чтобы множества белых точек этих фигур были подобны друг
другу и множества чёрных точек также были подобны друг другу (возможно
с различными коэффициентами подобия).
(Г. Гальперин)
Ответ: можно.
Решение.
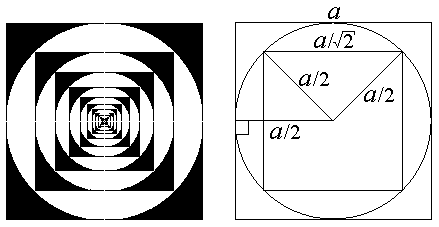
Рассмотрим такую раскраску квадрата: впишем круг в квадрат и раскрасим в чёрный цвет точки квадрата, лежащие вне круга; впишем в полученный круг квадрат со сторонами, параллельными сторонам исходного квадрата. Раскрасим в белый цвет точки круга, лежащие вне "маленького" квадрата. По такому же правилу раскрасим маленький квадрат и т. д. Заметим, что мы считаем граничные точки лежащими "внутри" фигуры. Таким образом, граница каждого квадрата покрашена чёрным, за исключением четырёх точек касания вписанного в квадрат круга, а граница каждого круга - белым, за исключением четырёх вершин квадрата, вписанного в этот круг.
Пусть сторона исходного квадрата равна a, тогда сторона маленького квадрата равна a/21/2. Следовательно, длины сторон квадратов стремятся к 0. Поэтому все точки, кроме центра, будут раскрашены. Центр раскрасим в чёрный цвет.
Очевидно, что множество чёрных точек квадрата подобно множеству чёрных точек круга, вписанного в этот квадрат (второе получается из первого гомотетией с центром в центре квадрата и с коэффициентом 1/21/2. А множество белых точек квадрата просто совпадает с множеством белых точек вписанного в него круга.