1. На острове 2/3 всех мужчин женаты и 3/5 всех женщин замужем.К
акая доля населения острова состоит в браке?
(В. Гуровиц)
Ответ: 12/19 населения острова.
Решение. Пусть число супружеских пар на острове равно N, то есть замужем N женщин, женаты N мужчин. Замужние женщины составляют 3/5 всех женщин острова, значит, на острове (5/3)N женщин. Женатые мужчины составляют 2/3 всех мужчин острова, значит, на острове (3/2)N мужчин. Всего на острове (5/3)N+(3/2)N=(19/6)N жителей, а в браке состоит 2N жителей. Искомая доля равна (2N)/((19/6)N)=12/19.
2. Квадрат суммы цифр числа A равен сумме цифр
числа A2. Найдите все такие двузначные числа A.
(А. Блинков)
Ответ: 10, 11, 12, 13, 20, 21, 22, 30, 31.
Решение 1. Заметим, что A2<992=9801<9999. Поэтому сумма цифр A2 меньше 9*4=36. Так как она равна квадрату суммы цифр A, то сумма цифр A меньше 361/2=6, то есть меньше или равна 5. Остаётся 15 вариантов: 10, 11, 12, 13, 14, 20, 21, 22, 23, 30, 31, 32, 40, 41, 50, из которых условию удовлетворяют только 9 вариантов, указанных в ответе.
Решение 2. Обозначим через S(n) сумму цифр числа n. Заметим, что при сложении двух чисел "столбиком" возможен только перенос единицы в старший разряд, и каждый такой перенос уменьшает сумму цифр на 9. Поэтому сумма цифр суммы любого количества слагаемых не превосходит суммы цифр слагаемых. Как следствие, S(n)<n, так как n=1+1+...+1 (n единиц), причём равенство достигается лишь для однозначных чисел, ведь при прибавлении очередной единицы к сумме девяти единиц уже возникнет перенос. Кроме того, от дописывания справа нуля сумма цифр не меняется, то есть S(10n)=S(n).
Пусть искомое двузначное число
A=ab=10a+b.
Тогда
S(A2)=S((10a+b)2)=S(100a2+10*2ab+b2)<
<S(100a2)+S(10*2ab)+S(b2)=S(a2)+S(2ab)+S(b2)<
<a2+2ab+b2=(a+b)2=(S(A))2,
причём равенство достигается тогда и только тогда, когда
a2, 2ab и b2 - однозначные числа
(если это так, то при сложении 100a2, 10*2ab и
b2 переносов не происходит, так как они содержат все свои
ненулевые цифры в разных разрядах).
Итак, необходимо и достаточно, чтобы числа a2,
b2 и 2ab были меньше 10, то есть
1<a<3, 0<b<3
и ab<4.
Отсюда находим все перечисленные в ответе варианты.
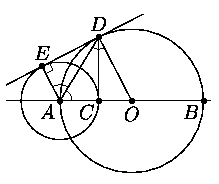
3. Дана окружность с диаметром AB. Другая окружностьс
центром в A пересекает отрезок AB в точке C,
причём AC<(1/2)AB. Общая касательная двух окружностей
касается первой окружности в точке D. Докажите, что прямая CD
перпендикулярна AB.
(А. Заславский)
Решение. Обозначим через E точку касания второй
окружности с общей касательной, через O - центр первой окружности
(см. рис.). Треугольник AOD - равнобедренный, поэтому
/ODA=/OAD. Так как OD||AE, то
/DAE=/ODA, откуда
DDEA=DDCA
(по двум сторонам и углу между ними). Значит,
/DCA=/DEA=90o и прямые DC
и AB перпендикулярны.

Замечание. Легко проверить, что утверждение задачи остаётся верным при любом радиусе второй окружности, меньшем AB.
4. Двое игроков по очереди выставляют на доску 65*65 по одной
шашке. При этом ни в одной линии (горизонтали или вертикали) не должно быть
больше двух шашек. Кто не может сделать ход - проиграл. Кто выигрывает при
правильной игре?
(А. Бучин, А. Иванищук)
Ответ: выигрывает второй.
Решение 1. Пусть первый поставил на доску первую шашку. Заметим, что от перестановки горизонталей доски ничего не изменяется. То же относится и к перестановке вертикалей. Поэтому будем считать, что второму игроку дополнительно разрешается менять местами любые горизонтали и вертикали.
После первого хода первого игрока второй игрок переставит горизонтали и вертикали так, чтобы первая шашка оказалась в средней вертикали, но не в центре доски.
Далее он должен делать ходы симметрично ходам первого игрока относительно центра доски. Тогда вторая шашка тоже окажется в средней вертикали, и первый не сможет занять центральную клетку. Легко проверить, что второй всегда сможет сделать симметричный ход (отдельно следует рассмотреть случай хода в среднюю горизонталь).
Решение 2. Опишем эту игру по-другому. Есть два ряда по 65 точек в каждом (точки одного ряда обозначают горизонтали доски, точки другого - вертикали).
Постановке шашки на пересечение горизонтали и вертикали соответствует проведение отрезка, соединяющего точки, которые обозначают эти горизонталь и вертикаль.
Таким образом, правила запрещают проводить из одной точки больше двух отрезков.
Второй игрок должен играть (за исключением последнего хода) так, чтобы после каждого его хода проведённые отрезки образовывали незамкнутую ломаную (возможно самопересекающуюся). Тогда после k-го хода второго игрока ломаная будет состоять из 2k звеньев и проходить через 2k+1 точку (k точек одного ряда и k+1 - другого). Поэтому первые 64 хода второй игрок всегда сможет продолжить ломаную или соединить её с отдельным отрезком, проведённым первым на предыдущем ходе. Последним, 65-м ходом, второй игрок должен соединить отрезком начало и конец ломаной, превращая её в замкнутую ломаную, проходящую через все 130 точек. После этого первый игрок не сможет сделать ход.
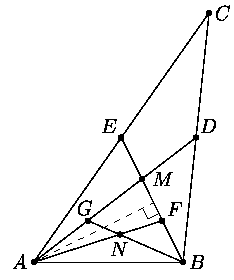
5. В треугольнике ABC медианы AD и BEп
ересекаются в точке M.
Докажите, что если угол AMB
а) прямой;
б) острый;
то AC+BC>3AB.
(И. Богданов)
Решение 1. Проведём в треугольнике AMB медианы AF
и BG и обозначим через N точку их пересечения (см. рис.).
Заметим, что MF=(1/2)MB=ME, так как M - точка
пересечения медиан - делит BE в отношении 2:1. Поскольку
/AMF<90, то основание перпендикуляра, опущенного
из вершины A на прямую BE, лежит на луче MB. Поэтому
AF<AE (равенство достигается в случае
/AMB=90o), так что
AN=(2/3)AF<(2/3)AE=(1/3)AC.
Аналогично, BN<(1/3)BC.
Используя неравенство треугольника, получаем требуемое неравенство:
AC+BC>3(AN+NB)>3AB.
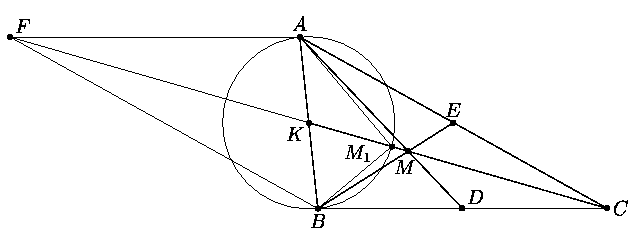
Решение 2. Проведём медиану CK и продолжим её на отрезок той же длины, получим точку F, такую что KF=CK (см. рис.). Четырёхугольник ACBF - параллелограмм. Из DACF имеем: AC+AF>FC=2CK, значит, AC+CB>2CK.
Построим на стороне AB как на диаметре окружность. Поскольку угол
AMB не тупой, точка M не лежит внутри этой окружности (это можно
понять, если рассмотреть точку M1 пересечения CK
с окружностью, угол AM1B - прямой,
а /AMB < /AM1B).
Значит, MK>M1K=AK=(1/2)AB.
Но CK=3MK, поэтому
AC+CB>2CK=6MK>3AB.
6. В клетчатом прямоугольнике m*n
каждая клетка может быть либо живой, либо мёртвой. Каждую минуту одновременно
все живые клетки умирают, а те мёртвые, у которых было нечётное число живых
соседей (по стороне), оживают.
Укажите все пары (m, n), для которых найдётся такая
начальная расстановка живых и мёртвых клеток, что жизнь в прямоугольнике
будет существовать вечно (то есть в каждый момент времени хотя бы одна клетка
будет живой)?
(А. Горбачёв)
Ответ: при всех парах чисел (m, n), кроме пар (1, 1), (1, 3) и (3, 1).
Решение. Достаточно рассмотреть случай m<n.
Пусть для некоторого n в прямоугольнике 1*n существует вечно
живая расстановка. Тогда такая расстановка существует и во всех
прямоугольниках m*n. Достаточно рассмотреть следующий вариант:
берём вечно живую расстановку 1*n и копируем её во все строки
прямоугольника m*n (см. рис., Ж - живая клетка, М - мёртвая).
ЖММЖЖММЖММ ЖММЖЖММЖММ ЖММЖЖММЖММ ЖММЖЖММЖММ ЖММЖЖММЖММ ЖММЖЖММЖММ ЖММЖЖММЖММ ^^^^^^^^^^ ЖММЖЖММЖММ
Тогда в нём столбцы будут эволюционировать так же, как клетки в соответствующем столбце прямоугольника 1*n. Действительно, все клетки живого столбца умирают, как и соответствующая клетка прямоугольника 1*n. У каждой клетки мёртвого столбца соседи сверху и снизу мертвы, поэтому количество её живых соседей равно количеству живых соседних столбцов, а значит, и количеству живых соседей у соответствующей клетки в прямоугольнике 1*n. Поскольку в нём всегда остаётся хотя бы одна живая клетка, то в построенной расстановке m*n всегда остаётся хотя бы один живой столбец.
Заметим, что при n=2 и n>4 вечно живые расстановки 1*n существуют: каждая из нижеперечисленных расстановок имеет период 2, то есть каждую вторую минуту возвращается в исходное состояние.
| n=2 : | ЖМ <-> МЖ | |
| чётное n>4 : | ЖММЖЖММЖ... <-> МЖЖММЖЖМ... | |
| нечётное n>4 : | ЖМММЖЖММЖ... <-> МЖМЖММЖЖМ... |
Кроме того, есть расстановка (также периода 2) в прямоугольнике 3*3:
ЖЖМ ММЖ МММ <-> ЖМЖ МЖЖ ЖММ
Тем самым, во всех прямоугольниках, кроме 1*1 и 1*3, примеры вечно живых
расстановок уже построены. Покажем, что в прямоугольниках 1*1 и 1*3 любая
расстановка рано или поздно умрёт. Случай 1*1 очевиден. Для случая 1*3 можно
считать (возможно, начиная отсчёт со второго шага), что первая клетка мертва.
Тогда остаётся 3 варианта, в которых есть хотя бы одна живая клетка. Эволюция
варианта МЖЖ включает в себя и МЖМ:
МЖЖ -> ЖММ -> МЖМ -> ЖМЖ -> МММ,
а вариант ММЖ симметричен варианту ЖММ, который также входит в рассмотренный
выше пример.