Закрытие олимпиады для 6-7 классов (Математического праздника) и награждение победителей (списки смотрите здесь) состоялось в день её проведения 18 февраля 2000 г.
Закрытие олимпиады для 8-11 классов классов состоится 18 марта 2001 г. в Главном здании МГУ на воробьевых горах.
12.00 - разбор задач; члены жюри расскажут решения задач, основные критерии проверки и ответят на Ваши вопросы.
13.00 - показ работ; школьники смогут посмотреть свою работу и узнать, за что поставлены именно такие оценки.
14.00 - лекцию для школьников прочтет академик РАН Д. В. Аносов.
16.00 - торжественное закрытие Олимпиады и награждение победителей.
Выдача нерозданных на закрытии грамот и призов - по средам (начиная с 21 марта) с 16.00 до 18.00 в каб. 202 МЦНМО (Большой Власьевский пер., 11). Тел. для справок 241-12-37.
Телефон для справок 241-12-37.
Условия
6 класс
1. Решите ребус: АX*УХ=2001.
(А. Блинков)
2. Офеня (продавец в разнос, коробейник) купил на
оптовом рынке партию ручек и предлагает покупателям либо одну
ручку за 5 рублей, либо три ручки за 10 рублей. От каждого
покупателя Офеня получает одинаковую прибыль. Какова оптовая
цена ручки?
(А. Саблин)
3. Наташа и Инна купили по одинаковой коробке чая в пакетиках.
Известно, что одного пакетика хватает на две или три чашки чая.
Наташе коробки хватило на только 41 чашку чая, а Инне - только на 58 чашек.
Сколько пакетиков было в коробке?
(А. Спивак, И. Ященко)
4. Расставьте по кругу 6 различных чисел так, чтобы каждое из них
равнялось произведению двух соседних.
(А. Митягин)
5. Вифсла, Тофсла и Хемуль играли в снежки. Первый снежок бросил
Тофсла. Затем в ответ на каждый попавший в него снежок Вифсла
бросал 6 снежков, Хемуль - 5, а Тофсла - 4 снежка. Через некоторое
время игра закончилась. Найдите, в кого сколько снежков попало,
если мимо цели пролетели 13 снежков. (В себя самого снежками не
кидаются.)
(Т. Голенищева-Кутузова, В. Клепцын)
6. Поля клетчатой доски размером 8*8 будем по очереди
закрашивать в красный цвет так, чтобы после закрашивания каждой
следующей клетки фигура, состоящая из закрашенных клеток, имела
ось симметрии. Покажите, как можно закрасить
а) 26;
б) 28 клеток, соблюдая это условие.
(В качестве ответа расставьте на тех клетках, которые должны быть
закрашены, числа от 1 до 26 или до 28 в том порядке, в
котором проводилось закрашивание.)
(И. Акулич)
7 класс
1. В книге рекордов Гиннесса написано, что наибольшее известное
простое число равно 23021377-1.
Не опечатка ли это?
(С. Маркелов)
2. Приходя в тир, игрок вносит в кассу 100 рублей. После каждого удачного выстрела количество его денег увеличивается на 10%, а после каждого промаха уменьшается на 10%. Могло ли после нескольких выстрелов у него оказаться 80 рублей 19 копеек? (И. Ященко)
3. Для постройки типового дома не хватало места. Архитектор
изменил проект: убрал 2 подъезда и добавил 3 этажа. При этом
количество квартир увеличилось. Он обрадовался и решил убрать еще
2 подъезда и добавить еще 3 этажа. Могло ли при этом квартир
стать даже меньше, чем в типовом проекте? (В каждом подъезде
одинаковое число этажей, а на всех этажах во всех подъездах одинаковое
число квартир.)
(T. Голенищева-Кутузова, В. Гуровиц, П. Кожевников, И. Ященко)
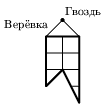
4. В стене имеется маленькая дырка (точка). У хозяина есть флажок
следующей формы (рис. 1). Покажите на рисунке все точки, в
которые можно вбить гвоздь, так чтобы флажок закрывал дырку.
(А. Шень)
5. Отметьте на доске 8*8 несколько клеток так, чтобы любая
(в том числе и любая отмеченная) клетка граничила по стороне
ровно с одной отмеченной клеткой.
(А. Спивак)
8 класс
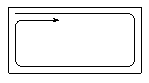
1. На клетчатой бумаге нарисован прямоугольник шириной 200 и
высотой 100 клеток. Его закрашивают по клеткам, начав с левой
верхней и идя по спирали (дойдя до края или уже закрашенной части,
поворачивают направо, рис. 2).
Какая клетка будет закрашена последней? (Укажите номер её строки
и столбца. Например, нижняя правая клетка стоит в 100-й строке
и 200-м столбце.)
(A. Хачатурян)
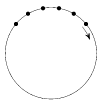
2. Можно ли поставить на плоскости 100 точек (сначала первую,
потом вторую и так далее до сотой) так, чтобы никакие три точки не лежали
на одной прямой и чтобы в любой момент фигура, состоящая из уже
поставленных точек, имела ось симметрии?
(И. Акулич)
3. Даны шесть слов:
ЗАНОЗА ЗИПУНЫ КАЗИНО КЕФАЛЬ ОТМЕЛЬ ШЕЛЕСТ
За один шаг можно заменить любую букву в любом из этих слов на
любую другую (например, за один шаг можно получить из слова ЗАНОЗА
слово ЗКНОЗА. Сколько шагов нужно,
чтобы сделать все слова одинаковыми (допускаются бессмысленные)?
Приведите пример и докажите, что меньшим числом шагов обойтись
нельзя.
(В. Доценко, А. Шень)
4. В треугольнике ABC проведены биссектриса AK,
медиана BL и высота CM. Треугольник KLM равносторонний.
Докажите, что треугольник ABC равносторонний.
(Р. Женодаров)
5. Лёша задумал двузначное число (от 10 до 99). Гриша
пытается его отгадать, называя двузначные числа. Считается, что
он отгадал, если одну цифру он назвал правильно, а в другой
ошибся не более чем на единицу (например, если задумано число
65, то 65, 64 и 75 подходят, а 63, 76 и 56 - нет).
Придумайте способ, гарантирующий Грише успех за 22
попытки (какое бы число ни задумал Лёша).
(Фольклор)
6. (Продолжение.) Покажите, что нет способа, гарантирующего Грише
успех за 18 попыток.
(Фольклор)
9 класс
1.
Можно ли расставить на футбольном поле четырёх футболистов так,
чтобы попарные расстояния между ними равнялись 1, 2, 3, 4, 5 и 6
метров?
(А. Митягин)
2.
В некоторой стране суммарная зарплата 10% самых высокооплачиваемых
работников составляет 90% зарплаты всех работников. Может ли так быть,
что в каждом из регионов, на которые делится эта страна,
зарплата любых 10% работников составляет не более
11% всей зарплаты, выплачиваемой в этом регионе?
(М. Вялый)
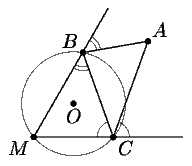
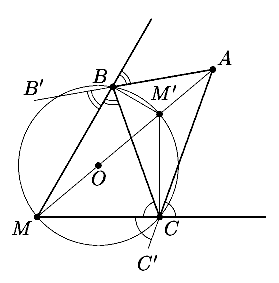
3. Внутри угла с вершиной M отмечена точка A.
Из этой точки выпустили шар, который отразился от одной стороны угла в
точке B, затем от другой стороны в точке C и вернулся
в A ("угол падения" равен "углу отражения", рис. 3).
Докажите, что центр O окружности, описанной около треугольника
BCM, лежит на прямой AM.
(А. Заславский)
4.
Камни лежат в трёх кучках: в одной - 51 камень, в другой - 49 камней,
а в третьей - 5 камней. Разрешается объединять любые кучки в одну,
а также разделять кучку из чётного количества камней на две равные.
Можно ли получить 105 кучек по одному камню в каждой?
(В. Клепцын)
5. Натуральное число N в 999...99
(k девяток) раз больше суммы своиx цифр. Укажите все возможные
значения k и для каждого из них приведите пример такого числа.
(Г. Гальперин)
6.
Участники шахматного турнира сыграли друг с другом по одной партии.
Для каждого участника A было подсчитано число набранных им
очков (за победу дается 1 очко, за ничью - 1/2 очка, за поражение - 0 очков)
и коэффициент силы по формуле: сумма очков тех участников, у кого
A выиграл, минус сумма очков тех, кому он проиграл.
а) Могут ли коэффициенты силы всех участников быть больше 0?
б) Могут ли коэффициенты силы всех участников быть меньше 0?
(А. Толпыго)
10 класс
1. Существуют ли три квадратных трёхчлена, такие что каждый из них имеет корень, а сумма любых двух трёхчленов не имеет корней? (А. Канель)
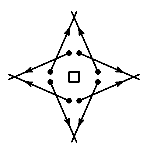
2. Можно ли расставить охрану вокруг точечного объекта так,
чтобы ни к объекту, ни к часовым нельзя было незаметно подкрасться?
(Каждый часовой стоит неподвижно и видит на 100 м строго вперёд.)
(В. Клепцын)
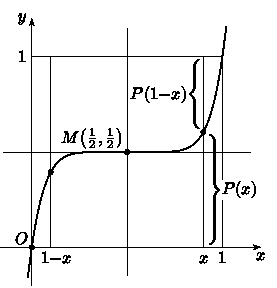
3. Приведите пример многочлена P(x) степени 2001, для которого выполняется тождество
P(x)+P(1-x)=1.
(В. Сендеров)
4. В остроугольном треугольнике ABC проведены высоты
AHA, BHB и
CHC. Докажите, что треугольник с вершинами в
точках пересечения высот треугольников
AHBHC,
BHAHC,
CHAHB равен треугольнику
HAHBHC.
(А. Акопян)
5. На двух клетках шахматной доски стоят чёрная и белая фишки.
За один ход можно передвинуть любую из них на соседнюю по вертикали или
горизонтали клетку (две фишки не могут стоять на одной клетке). Могут ли
в результате таких ходов встретиться все возможные варианты расположения
этих двух фишек, причём ровно по одному разу?
(А. Шаповалов)
6. В игре "Десант" две армии захватывают страну. Они ходят по
очереди, каждым ходом занимая один из свободных городов. Первый свой город
армия захватывает с воздуха, а каждым следующим ходом она может
захватить любой город, соединённый дорогой с каким-нибудь уже занятым
этой армией городом. Если таких городов нет, армия прекращает боевые
действия (при этом, возможно, другая армия свои действия продолжает).
Найдётся ли такая схема городов и дорог, что армия, ходящая второй, сможет
захватить более половины всех городов, как бы ни действовала первая армия?
(Число городов конечно, каждая дорога соединяет ровно два города.)
(П. Грозман, А. Шаповалов, Д. Шаповалов)
11 класс
1. Существуют ли три квадратных трёхчлена, такие что каждый из них
имеет два различных действительных корня, а сумма любых двух трёхчленов
не имеет действительных корней?
(А. Канель)
2. Дана геометрическая прогрессия.
Известно, что её первый, десятый и тридцатый члены
являются натуральными числами.
Верно ли, что её двадцатый член также является натуральным числом?
(Фольклор)
3. В треугольнике ABC точка I - центр вписанной
окружности, I' - центр окружности, касающейся стороны AB
и продолжений сторон CB и CA; L и L' - точки,
в которых сторона AB касается этих окружностей. Докажите, что прямые
IL', I'L и высота CH треугольника ABC
пересекаются в одной точке.
(А. Заславский)
4. Докажите, что не существует многочлена степени не ниже двух
с целыми неотрицательными коэффициентами, значение которого
при любом простом p является простым числом.
(А. Канель)
5. Докажите, что в пространстве существует расположение
2001 выпуклого многогранника, такое что никакие три из многогранников
не имеют общих точек, а любые два касаются друг друга (т. е. имеют
хотя бы одну граничную точку, но не имеют общих внутренних точек).
(А. Канель)
6. По кругу расставлено несколько коробочек. В каждой из них
может лежать один или несколько шариков (или она может быть пустой).
За один ход разрешается взять все шарики из любой коробочки и разложить
их, двигаясь по часовой стрелке, начиная со следующей коробочки, кладя
в каждую коробочку по одному шарику.
а) Докажите, что если на каждом следующем ходе шарики берут из
той коробочки, в которую попал последний шарик на предыдущем ходе,
то в какой-то момент повторится начальное размещение шариков.
б) Докажите, что за несколько ходов из любого начального
размещения шариков по коробочкам можно получить любое другое.
(В. Гуровиц)
Решения
6 класс
1. Ответ: АХ=29, УХ=69 или, наоборот, АХ=69, УХ=29. Поскольку 2001=3*23*29, число 2001 можно представить в виде произведения двузначных чисел лишь следующими способами: 69*29 или 23*87.
2. Ответ: оптовая цена ручки - 2 рубля 50 копеек. Если оптовая цена ручки - x рублей, то 5-x=10-3x, откуда x=2,5.
3. Ответ: 20 пакетиков.
Первое решение. Поскольку Инна выпила на 17 чашек чая больше Наташи, значит, хотя бы из 17 пакетиков она приготовила по три чашки чая. Оставшиеся 7=58-17*3 чашек можно было получить только одним способом: 2 пакетика на 2 чашки каждый и 1 пакетик на 3 чашки. Значит, в коробке было 17+3=20 пакетиков. При этом Наташа из 19 пакетиков приготовила по 2 чашки, а из двадцатого - 3 чашки чая.
Второе решение. Заметим, что пакетиков не могло быть больше 20: если бы в пачке был хотя бы 21 пакетик, Наташа не смогла бы выпить меньше 2*21=42 чашек чая. Но пакетиков не могло быть и меньше 20, иначе Инна выпила бы не больше 3*19=57 чашек. Значит, в каждой пачке могло быть только 20 пакетиков. Инна использовала по 3 раза 18 пакетиков, а Наташа - только 1.
4. Если рядом стоят числа a и b, то следующим стоит число b/a, за ним 1/a, потом 1/b, наконец, a/b. Эти шесть чисел удовлетворяют условию задачи. Конечно, при неудачном выборе чисел a и b какие-то из указанных чисел совпадут, но нас это не остановит: для решения задачи достаточно предъявить один пример. Например, взять a=2, b=3.
5. Ответ: в Хемуля, Вифслу и Тофслу попали по одному разу. Если в Вифслу, Тофслу и Хемуля попали x, y и z снежков соответственно, то всего было брошено 13+x+y+z снежков (поскольку 13 снежков не достигли цели). С другой стороны, Вифсла бросил 6x, Хемуль - 5y, а Тофсла - 4z+1 снежков (вместе с первым снежком). Получаем уравнение
6x+5y+4z+1=13+x+y+z, откуда 5x+4y+3z=12. Так как x, y, z - целые неотрицательные числа, x может быть равен 0, 1 или 2, y - 0, 1, 2 или 3, z - 0, 1, 2, 3 или 4. Перебором находим решения (1,1,1), (0,3,0) и (0,0,4). Но, поскольку в самого себя кидать снежки нельзя, то среди чисел x, y, z не может быть двух нулей. Поэтому возможен только первый случай.
6. Ответ приведён на рисунке.
| 1 | 20 | 13 | |||||
| 2 | 21 | 12 | |||||
| 3 | 22 | 11 | |||||
| 14 | 15 | 16 | 4 | 17 | 18 | 19 | 27 |
| 10 | 23 | 5 | |||||
| 9 | 24 | 6 | |||||
| 8 | 25 | 7 | |||||
| 26 | 28 |
7 класс
1. Ответ: конечно, это опечатка. Любая степень числа, оканчивающегося цифрой 1, тоже оканчивается цифрой 1. Поэтому разность 23021377-1 оканчивается на 0 и, следовательно, не является простым числом.
На самом деле наибольшим известным сегодня простым числом является число 23021377-1. Простые числа вида 2n-1 называют числами Мерсенна (по имени математика 17 века М. Мерсенна, который их исследовал). Можно доказать, что при составном n число 2n-1 составное. Поэтому числа Мерсенна соответствуют простым n. Например, 22-1=3, 25-1=31, 27-1=127 - простые числа. Однако нельзя утверждать, что каждому простому числу p соответствует простое число 2p-1. Например, 211-1 - составное число. Поиском чисел Мерсенна занимались многие выдающиеся математики, например, Эйлер доказал, что число 231-1 простое. Конечно или бесконечно множество чисел Мерсенна - вопрос, на который пока нет ответа.
2. Ответ: да, могло, если он один раз попал и три раза промахнулся. Решение проще всего найти, если разложить 8019 на множители: 8019=93*11. После удачного выстрела количество денег умножается на 1,1, а после неудачного - на 0,9, и 100*1,1*0,93=80,19.
3. Ответ: да, могло. Например, если в исходном проекте было 5 подъездов, 4 этажа и на каждом этаже по одной квартире: 5*4=20, 3*7=21, 1*10=10.
4. Ответ приведён на рисунке.
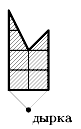
5. Пример приведён на рисунке.
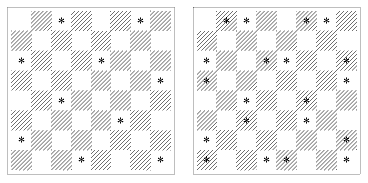
Будем рассуждать, используя шахматную доску. Заметим, что белые клетки граничат по стороне только с чёрными и наоборот. Поэтому сначала отметим несколько белых клеток, так чтобы у каждой чёрной клетки был ровно один отмеченный сосед (рисунок). Затем отметим несколько чёрных клеток, так чтобы и у каждой белой клетки появился отмеченный сосед (рисунок), при этом у чёрных клеток новых отмеченных соседей не появится.
8 класс
1. Ответ: клетка, расположенная в строке 51 и столбце 50. Сначала будет закрашен наружный слой клеток, после чего останется прямоугольник 98*198 клеток. Этот прямоугольник также будет закрашиваться по спирали; после покраски его наружного слоя останется прямоугольник 96*196 клеток и так далее. После окраски 49 слоёв незакрашенным останется прямоугольник 2*102, расположенный в строках 50-51 и столбцах 50-151. Последней будет закрашена нижняя левая клетка этого прямоугольника.
2. Ответ: да.
Можно, например, ставить точки на окружности через равные
достаточно малые интервалы (как на рисунке, только меньшие).
3. Ответ: 25. Напишем слова в столбик:
ЗАНОЗА ЗИПУНЫ КАЗИНО КЕФАЛЬ ОТМЕЛЬ ШЕЛЕСТПосле всех замен буквы в каждой колонке должны стать одинаковыми. Число замен будет наименьшим, если в каждой колонке сохранить наиболее частую букву (любую из них, если таких букв несколько). Например, в первой колонке можно оставить буквы З или К, они обе требуют четырёх замен. Минимальное число замен равно 4+4+5+4+4+4=25.
Среди слов, которые могут получиться в результате, есть осмысленные, например ЗЕЛЕНЬ, КАПЕЛЬ или КАФЕЛЬ.
4. Напомним, что в прямоугольном треугольнике медиана,
проведенная к гипотенузе, равна её половине и, наоборот, если медиана
равна половине стороны, к которой она проведена, то треугольник прямоугольный.
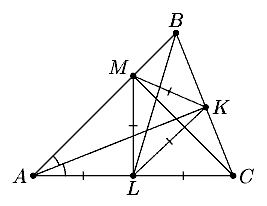
Медиана ML прямоугольного треугольника AMC равна половинам гипотенузы AL и LC, а также отрезкам KL и KM, так как стороны треугольника KLM равны (см. рис.). В треугольнике AKС медиана KL равна половине стороны AC, поэтому угол AKC прямой и в треугольнике ABC биссектриса AK является высотой. Следовательно, треугольник ABC равнобедренный (AB=BC) и AK является также медианой: BK=KC. Значит, MK - медиана прямоугольного треугольника BMC, поэтому BC=2MK=2KL=AC. Итак, AB=BC=AC, что и требовалось доказать.
5, 6. Расположим двузначные числа в клетках прямоугольника высоты 9 и ширины 10 (по горизонтали откладываем единицы, по вертикали - десятки).
Каждой попытке Гриши соответствует крестик из пяти клеток (см. рис.): в центре названное им число, а по бокам четыре числа, отличающиеся в одной цифре на единицу (если названное число содержит цифру 0 или 9, некоторые клетки крестика выходят за края прямоугольника; таким клеткам никакие числа не соответствуют). Задача Гриши - покрыть прямоугольник 9*10 такими крестиками. Убедимся, что 22 крестиков ему хватит, а 18 крестиков - нет.
Покрытие из 22 крестиков легко найти, если заметить, что
крестиками можно выложить плоскость без перекрытий (правда, придётся ещё
добавить несколько крестиков по краям прямоугольника).
Например, Гриша может назвать числа
11, 13, 17, 25, 29, 30, 32, 37, 44, 49, 51, 56, 63, 68, 70, 75,
82, 87, 89, 90, 94, 97.
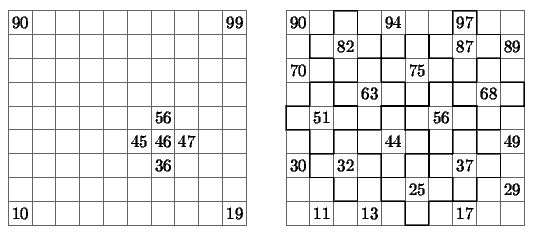
В задаче 6 суммарная площадь крестиков равна 18*5=90, т. е. равна площади прямоугольника. Но, покрывая угловую клетку, мы неизбежно выйдем за пределы прямоугольника, и эта потеря помешает покрыть весь прямоугольник.
9 класс
1. Ответ: да, можно. Расставим их на одной прямой так, чтобы расстояние между первым и вторым футболистами было 2 м, между вторым и третьим - 3 м, между третьим и четвертым - 1 м (футболисты назывались в порядке их расположения на прямой).
2. Ответ: да, может. Допустим, что в каждом регионе все получают одинаковую зарплату и есть регион, в котором живут те самые 10% работников, которые получают 90% всей зарплаты.
3. Перпендикуляры к сторонам угла, восставленные в
точках B и C, пересекаются в точке M', диаметрально
противоположной M. Из равенства углов падения и отражения следует,
что M' - точка пересечения биссектрис треугольника ABC.
С другой стороны, точка M лежит на пересечении биссектрис углов
B'BC и BCC'(см. рис.), следовательно, равноудалена
от прямых AB и AC. Поэтому M также лежит на биссектрисе
угла BAC. Значит, весь диаметр MM', включая точку O,
лежит на биссектрисе AM угла BAC.
4. Ответ: нет, нельзя. Заметим, что если в некоторый момент количество камней в каждой кучке делится на нечётное число a, то и во всех получаемых разрешёнными действиями кучках количество камней будет делиться на a. После первого хода можно получить три варианта размещения камней: кучки из 100 камней и 5 камней (общий делитель 5), из 56 камней и 49 камней (общий делитель 7), из 51 камня и 54 камней (общий делитель 3).
5. Ответ: такое число существует для любого k:
Nk=9k*(10k-1).
Пусть
9k=s1...st0...0
(st не равно 0, нулей на конце может и не быть).
Проверим, что сумма цифр числа Nk равна 9k.
Запишем разность чисел 9k*10k и 9k, учитывая,
что 9k<10k при любом k:
| - | s1s2...st-1 | st | 0...0 | 0 | ... | 0 | 0 | 0...0 |
| s1 | ... | st-1 | st | 0...0 | ||||
| s1s2...st-1 | st-1 | 9...9 | (9-s1) | ... | (9-st-1) | (10-st) | 0...0 |
s1+...+st-1+9+...+9+(9+1)-s1-...-st=9k.
в записи левой части k девяток)
6. Ответ: а), б) нет, не могут. Обозначим сумму очков, набранных участником A, через SA, а его коэффициент силы - через FA. Рассмотрим сумму SASAFA. Если подставить в неё определение FA и раскрыть скобки, то получится сумма чисел вида +SASB, где шахматисты A и B сыграли не вничью. Каждое из таких слагаемых входит один раз со знаком "+" и один раз со знаком "-". Поэтому вся сумма равна 0. Значит, знаки коэффициентов силы у всех участников не могут быть одинаковыми.
10 класс
1. Ответ: да, существуют. Например, таковыми являются многочлены x2, (x-1)2 и (x-2)2. Сумма любых двух из них больше нуля при любом x.
2. Ответ: да, можно. На рисунке показан пример
расположения восьми часовых, удовлетворяющий условию. Кружочками
обозначены часовые, каждая из стрелок указывает направление,
в котором смотрит часовой.
3. Например,
P(x)=22000(x-(1/2))2001+(1/2).
График этой функции (рис.) получается из графика нечётной функции
y=x2001 сдвигом вправо на 1/2, растяжением и
сдвигом вверх на 1/2 и поэтому имеет центр симметрии
M(1/2; 1/2). Теперь легко понять, что
P(1-x)=1-Px).
4. Пусть H1, H2,
H3 - ортоцентры (точки пересечения высот) треугольников
AHBHC,
BHAHC,
CHAHB соответственно,
H - ортоцентр треугольника ABC, M1,
M2, M3 - середины
HBHC,
HCHA и
HAHB.
Покажем, что точка Hi симметрична точке
H относительно Mi
(i=1, 2, 3). Рассмотрим, например, точку H2.
Поскольку
HCH2 | BC и
AH | BC, отрезки
HCH2 и
HHA параллельны (см. рис.).
Аналогично, HAH2||HHC. Значит, HCH2HAH - параллелограмм и точка H2 симметрична H относительно середины стороны HAHC. Такие же рассуждения справедливы для точек H1 и H3.
Получаем конфигурацию, показанную на рисунке.
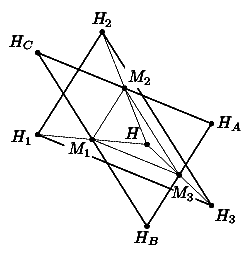
Так как M1M2 - общая средняя линия треугольников HAHBHС. и H1H2H отрезки HAHB и H1H2 равны. Аналогично доказываются равенства HBHC=H2H3 и HAHC=H1H3. Следовательно, треугольники H1H2H3 и HAHBHC равны.
5. Ответ: не могут. Назовём расположение фишек одноцветным, если фишки стоят на клетках одного цвета, разноцветным - если на клетках разного цвета. Заметим, что при перемещениях фишек одноцветные и разноцветные расположения чередуются, значит, их должно быть поровну. Однако общее количество разноцветных расположений равно 2*322, а одноцветных - 2*32*31, поскольку две фишки не могут стоять на одной клетке. Значит, все возможные расположения встретиться не могут.
6. Ответ: да, найдётся. Рассмотрим страну, карта которой
изображена на рисунке (точки - города, отрезки - дороги).
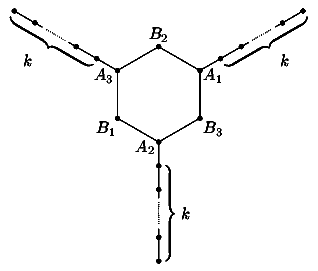
Покажем, что второй армии всегда удастся захватить хотя бы две точки Ai. Действительно, если первая армия первым ходом занимает точку на "ветке" из k точек, вторая армия должна занять соответствующую этой "ветке" точку Ai; если первая занимает Ai, то вторая - Bi; если первая выбирает точку Bi, то вторая - одну из точек Aj, соединенную отрезком с Bi. Дальнейшие действия очевидны.
Так как после прекращения боевых действий вторая армия занимает хотя бы две точки Ai, первая занимает не более k+3 точек. Поэтому доля городов, захваченных второй армией, не менее (2k+3)/(3k+6). Уже при k=1 это число больше 1/2. Заметим, что в условии задачи вместо 1/2 можно взять любое число a<2/3: при достаточно больших k число (2k+3)/(3k+6) будет больше a.
11 класс
1. Ответ: да, существуют. Например, таковыми являются многочлены (x-10)2-1, x2-1 и (x+10)2-1.
2. Ответ: да, верно. Пусть a1, a2, ..., a_n, ... - данная геометрическая прогрессия, q - её знаменатель. По условию a1, a10=a1q9 и a30=a1q29 - натуральные числа. Поэтому q9 и q29 - положительные рациональные числа. Отсюда следует, что q2=q29/(q9)3 - положительное рациональное число и q=q9/(q2)4 также положительное рациональное число.
Пусть q=m/n, где m и n - натуральные взаимно простые числа. Число a30=a1m29/n29 натуральное, m29 и n29 взаимно просты, следовательно, a1 делится на n29. Отсюда получаем, что a20=a1q19=a1m19/n19 - число натуральное.
3.
Обозначим через M точку вписанной окружности, диаметрально
противоположную точке L, через M' - точку вневписанной
окружности, диаметрально противоположную точке L' (рис.).
Таким образом, ML и M'L' - диаметры, соответственно,
вписанной и вневписанной окружностей, они параллельны высоте CH
треугольника ABC. Вписанная окружность переходит во вневписанную
при гомотетии с центром в точке C. При этой гомотетии диаметр
ML переходит в параллельный ему диаметр, т. е. M'L'.
Поэтому точки C, M, L' лежат на одной прямой, а также
точки C, M', L лежат на одной прямой.
Отсюда следует, что треугольники L'LM и
L'HC совмещаются гомотетией с центром в точке L'.
Поскольку L'I - медиана треугольника L'LM,
прямая L'I пересекает отрезок CH в его середине.
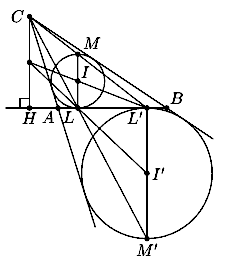
Далее, треугольники LL'M' и LHC совмещаются гомотетией с центром в точке L. Поскольку LI' является медианой в треугольнике LL'M', прямая LI' также пересекает отрезок CH в его середине, откуда следует утверждение задачи.
4. Предположим, что такой многочлен Q(x) существует. Пусть Q(x)=anxn+an-1xn-1+...+a1x+a0, где a0, a1, ..., an - целые неотрицательные числа, an не равно 0, n>2.
Если a0=0, то Q(x)=x(anxn-1+an-1xn-2+...+a1), следовательно, при простом p число Q(p) делится на p и больше p (здесь используется то, что степень Q не меньше 2), поэтому Q(p) - число составное. Допустим, a0>2. Обозначим через p некоторый простой делитель a0. Тогда Q(p)=(anpn-1+an-1pn-2+...+a1)p+a0 делится на p и больше p, значит, Q(p) - число составное. Таким образом, имеется единственная возможность: a0=1.
Если для любого простого p число Q(p) простое, то и число Q(Q(p)) является простым при любом простом p). Значит, свободный член многочлена Q(Q(x)) должен равняться 1. Однако, поскольку Q(0)=a0=1, Q(Q(0))=an+an-1+...+a1+1>1. Мы получили противоречие, завершающее доказательство.
5. Положим N=2001 и опишем построение расположения N выпуклых многогранников, из которых никакие три не пересекаются и любые два касаются.
Рассмотрим бесконечный круговой конус, вершина O которого
находится в начале координат, а ось направлена вдоль оси Oz.
На окружности, являющейся сечением конуса плоскостью z=1,
возьмём точки A1, A2, ...,
AN - вершины правильного N-угольника.
Обозначим через B1, B2, ...,
BN середины меньших дуг
A1A2,
A2A3, ...,
ANA1 соответственно.
Через C(t) обозначим круг, являющийся сечением конуса
плоскостью z=t, через Ot -
центр этого круга, через
Ati,
Bti - точки пересечения
образующих OAi,
OBi с кругом C(t),
где t>0, 1<i<N.
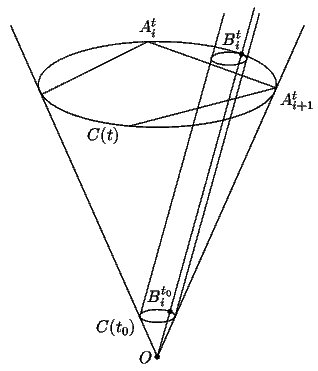
Докажем вспомогательное утверждение.
Лемма. Пусть выпуклый многоугольник M лежит внутри круга C(t0), t0>0. Рассмотрим бесконечную вверх "призму" P, основанием которой служит многоугольник M, а боковое "ребро" параллельно прямой OBi для некоторого i. Многоугольник (равный M), который получается при пересечении призмы P и круга C(t), обозначим M(t) (таким образом, M(t0) совпадает с M). Тогда найдётся такое положительное T>t0, что при всех t>T многоугольник M(t) будет содержаться внутри сегмента Si(t)=AtiBtiAti+1 круга C(t).
Доказательство. Многоугольник M(t) является образом M при параллельном переносе на вектор, параллельный образующей OBi. Поэтому многоугольник M(t) содержится внутри круга, равного кругу C(t0), который касается круга C(t) в точке Bi^t. Расстояние от точки Bi^t до прямой Ai^tA_{i+1}^t прямо пропорционально длине образующей OBti; следовательно, найдется такое T, что при всех t>T это расстояние больше диаметра окружности C(t0) (рис. xx). Это и означает, что многоугольник M(t) попадает внутрь сегмента Si(t) круга C(t). Лемма доказана.
Переходим к индуктивному построению нашего расположения.
Выберем t1>0. Возьмём выпуклый многоугольник M1 внутри круга C(t1). Рассмотрим бесконечную вверх "призму" P1, основанием которой служит многоугольник M1, а боковое "ребро" параллельно прямой OB1.
Пусть для некоторого n (1<n<N) уже определены положительные числа t1, t2, ..., tn-1, t1<t2<...<tn-1, выпуклые многоугольники M1, ..., Mn-1, лежащие внутри кругов С(t1), С(t2), ..., С(tn-1), бесконечные "призмы" P1, P2, ..., Pn-1 с основаниями M1, M2, ..., Mn-1 и боковыми "рёбрами", параллельными OB1, OB2, ..., OBn-1 соответственно.
Согласно лемме, существует число tn>tn-1, такое что многоугольник M1(tn) содержится внутри сегмента S1(tn) круга C(tn), многоугольник M2(tn) содержится внутри сегмента S2(tn) круга C(tn), ..., многоугольник Mn-1(tn) содержится внутри сегмента Sn-1(tn) круга C(tn).
Сдвигаем каждую из прямых AtniAtni+1 (1<i<n-1) в направлении вектора OtnBtni, пока она не совпадёт с прямой li(tn), касающейся многоугольника Mi(tn). Теперь построим выпуклый многоугольник Мn, который содержится в круге C(tn), касается каждого многоугольника Mi(tn) и лежит по разные с ним стороны от прямой li(tn): возьмём для каждого i одну из точек касания многоугольника Mi(tn) и прямой li(tn); при n>3 эти точки являются вершинами выпуклого (n-1)-угольника, который и можно выбрать в качестве Mn; при n=2, 3 надо добавить ещё несколько точек).
Рассмотрим бесконечную вверх "призму" Pn, основанием которой является многоугольник Mn, а боковое "ребро" параллельно прямой OBn. Построение будет закончено, когда мы получим призмы P1, P2, ..., PN. Наконец, "срежем" призмы плоскостью z=T, где T>tN.
Докажем, что полученные (обычные) призмы удовлетворяют условию задачи.
Для этого достаточно показать, что призма Pn
пересекается с призмой Pi, i<n,
только в плоскости круга C(tn). Пусть,
напротив, найдётся общая точка RCC(t) двух призм,
где t>tn.
Через точку R проведём прямые, параллельные
OBn и OBi;
обозначим их точки пересечения с плоскостью круга
C(tn) через Rn и
Ri соответственно. Тогда точка
Rn должна принадлежать многоугольнику
Mn(tn),
а точка Ri должна принадлежать многоугольнику
Mi(tn).
Ясно, что (ненулевые) векторы
RiRn и
BtniBtnn
противоположно направлены.
Однако это невозможно, поскольку точки Ri и Btni лежат по одну сторону от прямой li(tn), а точки Rn и Btnn - по другую. Противоречие завершает доказательство.
6. а) Текущее состояние описанной в задаче системы определяется количеством шариков в каждой коробочке и указанием коробочки, с которой нужно начинать раскладывать шарики в следующий раз. Поэтому возможных состояний системы конечное число. Из каждого состояния можно, раскладывая шарики, перейти в другое состояние системы, которое определено однозначно. Наоборот, зная состояние системы в настоящий момент, можно однозначно определить состояние системы перед последним раскладыванием шариков. Действительно, последнее раскладывание должно было закончиться на выделенной коробочке; поэтому, чтобы восстановить предыдущее состояние, нужно взять один шарик из выделенной коробочки и далее, идя против часовой стрелки, брать по шарику из каждой коробочки, пока это возможно. Когда же мы встретим пустую коробочку, мы положим в неё все собранные шарики и объявим её отмеченной. (Фактически мы дали описание операции, обратной к ходу, описанному в условии задачи.) Если обозначить состояния системы точками, а возможность перехода из одного состояния в другое - стрелкой, соединяющей соответствующие точки (т. е. построить граф состояний системы), то из каждой точки будет выходить ровно одна стрелка и в каждую точку будет входить ровно одна стрелка. Начнём двигаться по стрелкам, начиная с заданного состояния A1. Получаем последовательность состояний A2, A3... Поскольку число состояний конечно, в некоторый момент в последовательности {Ai} возникнет повторение. Пусть, например, Ak=An, где n<n. Поскольку в точку Ak входит ровно одна стрелка, из равенства Ak=An следует Ak-1=An-1, ..., A1=Ak-n+1 Тем самым, через n-k ходов мы вернулись в состояние A1.
б) В отличие от задачи а) теперь состояние системы определяется лишь тем, как разложены шарики по коробочкам. В каждый момент возможно несколько ходов, а именно столько, сколько в данный момент имеется непустых коробочек. Очевидно, имеется столько же возможностей выполнить обратную операцию, описанную в решении пункта а). В терминах графа состояний системы это означает, что из каждой точки выходит столько же стрелок, сколько в неё входит.
Докажем два вспомогательных утверждения.
1) При любом начальном состоянии можно добиться того, чтобы все шарики оказались в одной наперёд заданной коробочке M.
В самом деле, если при каждой операции брать шарики из непустой коробочки, ближайшей к M при движении против часовой стрелки, то либо число шариков в M увеличится, либо ближайшая к M непустая коробочка станет ещё ближе, что не может продолжаться бесконечно. Утверждение доказано.
Обозначим через K состояние, при котором все шарики собраны в коробочке M, и через B некоторое произвольное состояние.
2) Из B можно пройти в K, двигаясь по стрелкам против их направления (по обратным стрелкам).
Действительно, согласно предыдущему утверждению, найдётся такая последовательность (различных) состояний B=A1, A2, ..., An=K, что точки A1, A2, ..., An последовательно соединены стрелками. Будем двигаться по обратным стрелкам из An в An-1, из An-1 в An-2, ..., из A2 в A1 и далее из A1, пока это возможно, выбирая на каждом шаге обратную стрелку, по которой мы ещё не проходили. Остановиться мы можем только в K. В самом деле, предположим, что при движении мы стираем стрелки. Cначала в каждую точку входило столько же стрелок, сколько выходило из неё. При стирании стрелок в каждый момент времени в каждую точку, за исключением начальной точки K, входит не меньше стрелок, чем выходит. Следовательно, если мы вошли в некоторую точку (кроме K) по обратной стрелке, то мы сможем и выйти из неё. Отсюда следует, что из B можно пройти в K по обратным стрелкам, т. е. из K можно пройти в B по обычным стрелкам.
Теперь нетрудно завершить доказательство. Пусть имеются два произвольных состояния A и B. Чтобы пройти, двигаясь по стрелкам, из A в B, можно вначале пройти из A в K, а затем из K в B. Как мы доказали, и то и другое возможно.