Олимпиада состоялась 29 февраля 2004 года.
1. У квадратного уравнения x2+px+q=0 коэффициенты p и q увеличили на единицу. Эту операцию повторили четыре раза. Приведите пример такого исходного уравнения, что у каждого из пяти полученных уравнений корни были бы целыми числами.
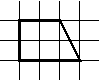
2. Разрежьте изображённую на рисунке трапецию на три части
и сложите из них квадрат.

3. В треугольнике ABC сторона AC наименьшая. На сторонах AB и CB взяты точки K и L, соответственно, такие что KA=AC=CL. Пусть M - точка пересечения AL и KC, а I - центр вписанной в треугольник ABC окружности. Докажите, что прямая MI перпендикулярна прямой AC.
4. Курс акций компании "Рога и копыта" каждый день в 12.00 повышается или понижается на n процентов, где n - фиксированное целое положительное число, меньшее 100 (курс не округляется). Существует ли n, для которого курс акций может дважды принять одно и то же значение?
5.
а) Из картона вырезали 7 выпуклых многоугольников и положили на стол так,
что любые 6 из них можно прибить к столу двумя гвоздями,
а все 7 нельзя.
Приведите пример таких многоугольников и их расположения.
(Многоугольники могут перекрываться.)
б) Из картона вырезали 8 выпуклых многоугольников и положили на стол так, что любые 7 из них можно прибить к столу двумя гвоздями, а все 8 --- нельзя. Приведите пример таких многоугольников и их расположения. (Многоугольники могут перекрываться.)
6.
На шахматную доску произвольным образом уложили 32 доминошки
(прямоугольника 1*2), так что доминошки не перекрываются.
Затем к доске добавили одну клетку, как показано на рисунке.
Разрешается вынимать любую доминошку, а затем класть её на
две соседние пустые клетки.
1.
Курс акций компании "Рога и копыта" каждый день в 12.00
повышается или понижается на 17 процентов (курс не округляется).
Может ли курс акций дважды принять одно и то же значение?
2.
У квадратного уравнения
x2+px+q=0
коэффициенты p и q увеличили на единицу.
Эту операцию повторили девять раз.
Могло ли оказаться, что у каждого из десяти полученных
уравнений корни --- целые числа?
3.
Бильярдный стол имеет форму многоугольника (не обязательно выпуклого),
у которого соседние стороны перпендикулярны друг другу.
Вершины этого многоугольника --- лузы, при попадании в которые шар
там и остаётся.
Из вершины с (внутренним) углом в 90o выпущен шар, который
отражается от бортов (сторон многоугольника) по закону
"угол падения равен углу отражения".
Докажите, что шар в эту вершину никогда не вернётся.
4.
Пусть la, lb и
lc --- длины биссектрис углов A,
B и C треугольника ABC, а
ma, mb и
mc --- длины соответствующих медиан.
Докажите, что
(la/ma)+
(lb/mb)+
(lc/mc)>1
5.
Назовём натуральное число разрешённым,
если оно имеет не более 20 различных простых делителей.
В начальный момент имеется куча из 2004!
(т. е. 1*2*...*2004) камней.
Два игрока по очереди забирают из кучи некоторое
разрешённое количество камней (возможно, каждый раз новое).
Побеждает тот, кто заберёт последние камни.
Кто выигрывает при правильной игре?
6.
Перед экстрасенсом лежит колода из 36 карт рубашкой вверх
(4 масти, по 9 карт каждой масти).
Он называет масть верхней карты, после чего карту открывают и показывают ему.
После этого экстрасенс называет масть следующей карты и т. д.
Задача экстрасенса --- угадать масть как можно большее число раз.
Рубашки карт несимметричны, и экстрасенс видит, в каком из
двух положений лежит верхняя карта. Помощник экстрасенса знает порядок карт
в колоде, не может менять его, но может расположить рубашку каждой
из карт тем или иным образом.
Мог ли экстрасенс так договориться с помощником, когда тот ещё не знал
порядок карт, чтобы обеспечить угадывание масти не менее чем
a) 19 карт;
б) 23 карты?
Если Вы придумали способ угадывания другого количества карт,
большего 19, то тоже напишите.
1.
Арифметическая прогрессия состоит из целых чисел.
Сумма первых n членов этой прогрессии является степенью двойки.
Докажите, что n --- также степень двойки.
2.
Существует ли тетраэдр, все грани которого --- равные
прямоугольные треугольники?
3.
Назовём белыми числа вида
4. Назовём натуральное 5.
Радиус описанной окружности треугольника ABC равен радиусу окружности,
касающейся стороны AB в точке C' и продолжений двух
других сторон в точках A' и B'.
Докажите, что центр описанной окружности треугольника ABC
совпадает с ортоцентром (точкой пересечения высот)
треугольника A'B'C'.
6. Перед экстрасенсом лежит колода из 36 карт рубашкой вверх
(4 масти, по 9 карт каждой масти).
Он называет масть верхней карты, после чего карту открывают и показывают ему.
После этого экстрасенс называет масть следующей карты и т. д.
Задача экстрасенса --- угадать масть как можно большее число раз.
Рубашки карт несимметричны, и экстрасенс видит, в каком из
двух положений лежит верхняя карта. Помощник экстрасенса знает порядок карт
в колоде, не может менять его, но может расположить рубашку каждой
из карт тем или иным образом.
Мог ли экстрасенс так договориться с помощником, когда тот ещё не знал
порядок карт, чтобы обеспечить угадывание масти не менее чем
a) 19 карт;
б) 23 карты?
Если Вы придумали способ угадывания другого количества карт,
большего 19, то тоже напишите.
1.
Докажите, что любой квадратный трёхчлен
можно представить в виде суммы двух квадратных трёхчленов
с нулевыми дискриминантами.
2.
Верно ли, что для любых четырёх попарно скрещивающихся прямых
можно так выбрать по одной точке на каждой из них, чтобы эти
точки были вершинами а) трапеции, б) параллелограмма?
3.
Докажите, что для любого натурального числа d
существует делящееся на него натуральное
число n, в десятичной записи которого можно вычеркнуть
некоторую ненулевую цифру так, что получившееся число тоже будет
делиться на d.
4.
Треугольник ABC с острым
углом /A=a
вписан в окружность. Диаметр этой окружности проходит через
основание высоты треугольника, проведённой из вершины B,
и делит треугольник ABC на две части
одинаковой площади. Найдите величину угла B.
5. Для заданных натуральных чисел
k0<k1<k2
выясните, какое наименьшее число корней на промежутке
sink0x+A1*sink1x+
A2*sink2x=0 6.
Вдоль стены круглой башни по часовой стрелке ходят два стражника,
причём первый из них --- вдвое быстрее второго.
В этой стене, имеющей длину 1, проделаны бойницы.
Система бойниц называется надёжной, если в каждый момент времени хотя бы
один из стражников находится возле бойницы.
а) Какую наименьшую длину может
иметь бойница, если система, состоящая только из этой бойницы, надежна?
б) Докажите, что суммарная длина бойниц любой надёжной системы
больше 1/2.
в) Докажите, что для любого числа s>1/2 существует
надёжная система бойниц с суммарной длиной, меньшей s.
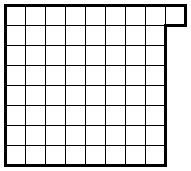
Докажите, что можно расположить все доминошки горизонтально.
9 класс
10 класс
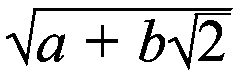 (a+b(21/2))1/2
(a+b(21/2))1/2
где a и
b --- целые, не равные нулю.
Аналогично, назовём чёрными числа вида
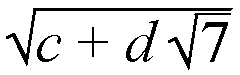 (c+d(71/2))1/2
(c+d(71/2))1/2
где c и d --- целые, не равные нулю.
Может ли чёрное число равняться сумме нескольких белых?
11 класс
![]()