Московская математическая олимпиада 2004/2005 учебного года.
Окружной тур.
Окружной тур для 5-7 классов проводился по школам (его могла организовать
у себя любая школа).
Рекомендованная оргкомитетом дата проведения
этого мероприятия - 22 января 2005 г.
Окружной тур для 8-11 классах проводился 30 января 2005 года во всех округах г.Москвы, кроме Центрального (в нем --- 29.01.05).
5 класс
5.1. Учительница предложила детям вычислить произведение чисел
415327 и 8373. Миша выполнил вычисления первым и получил ответ
328363624.
— Этот ответ неверный, — заметил Петя.
— Откуда ты это знаешь, если ты ещё не закончил свои вычисления? —
возмутился Миша.
— Тем не менее, я вижу, что этот ответ не может
быть правильным, — сказал Петя.
Кто из мальчиков прав?
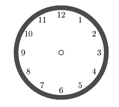
5.2. Разрежьте циферблат часов на три части так, чтобы
сумма цифр в каждой части была одинаковой.
5.3. В семье четверо детей. Им исполнилось 5, 8, 13 и 15 лет.
Детей зовут Аня, Миша, Вера и Женя. Одна из девочек
ходит в детский сад. Аня старше Миши. Сумма возрастов
Ани и Жени делится на 3. Кто Женя: мальчик или девочка?
5.4. Вася записал на доске два числа. Петя записал рядом их сумму.
Ваня сложил все три записанных числа, получил четвертое и записал его.
Чему равна сумма всех четырёх выписанных чисел, если Петя записал число 5?
5.5. Можно ли в таблице 8´8 закрасить 17 клеток так,
чтобы никакие две закрашенные клетки не оказались рядом (даже
по диагонали)? Решения.
5.1.Ответ: прав Петя.
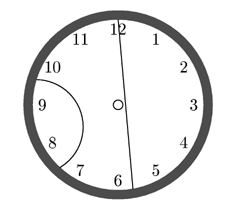
5.2.Ответ: например, см. рис.
5.3. Ответ: Женя — девочка.
5.4. Ответ: 20.
5.5. Ответ: Нет, нельзя.
6 класс
6.1. Туристическое агентство "Дуремар" предложило
Карабасу три путевки в "Страну дураков" —
две взрослых и одну детскую — за 3543 золотые монеты.
Известно, что детская путевка дешевле взрослой на 500 золотых монет.
Каким образом Карабас сумел понять, что его обманывают?
6.2. Покрасьте шесть клеток таблицы размером 6´6 в чёрный цвет так,
чтобы из неё нельзя было вырезать ни белой полоски размером 1´6,
ни белого квадрата размером 3´3.
6.3. Имеется три конверта, на один из которых нужно наклеить марку.
В каждом конверте содержится листок с двумя утверждениями.
В одном конверте оба утверждения истинны, в другом — оба ложны,
а в третьем конверте одно утверждение истинно, а другое — ложно.
Вот эти утверждения:
Конверт 1
1.1. На этот конверт не нужно наклеивать марку.
Конверт 2
2.1. Не нужно наклеивать марку на первый конверт.
Конверт 3
3.1. Не следует наклеивать марку на этот конверт.
Определите, на какой конверт нужно наклеить марку.
6.4. В некотором трёхзначном числе поменяли местами две последние цифры и
сложили полученное число с исходным. Получилось четырёхзначное число,
начинающееся на 195. Какой могла быть последняя цифра исходного числа?
6.5. Из Простоквашино в Ромашково выехал почтальон Печкин.
Одновременно из Ромашково в Простоквашино вышел кот Матроскин.
После их встречи Печкин повернул обратно, а кот Матроскин продолжил свой путь.
Почтальон Печкин вернулся в Простоквашино на 30 минут раньше Матроскина,
а его скорость была в 6 раз больше скорости кота. Сколько времени затратил
на путь из Ромашково в Простоквашино кот Матроскин? Решения.
6.1. Первый способ. Если бы стоимость детской путевки была равна
стоимости взрослой, то три путевки стоили бы 3543+500=4043
золотые монеты. Но это число не делится на три.
6.2.Ответ: например, см. рис.
6.3.Ответ:на третий конверт.
6.4.Ответ: 5, 6, 7, 8, 9.
6.5.Ответ: 42 минуты.
7 класс
7.1. Существуют ли такие два числа, что их сумма равна их произведению и
равна частному
от деления одного из этих чисел на другое?
7.2. Гонцу надо было пробежать 24 мили.
Две трети этого расстояния он бежал со средней скоростью 8 миль в час.
Сможет ли он, увеличив скорость, пробежать остаток пути так, чтобы
его средняя скорость на всем пути оказалась равной 12 миль в час?
7.3. Даны точки А, B, C и D такие, что отрезки
АC и BD пересекаются в точке E.
Отрезок АЕ на 1 см короче, чем отрезок АВ, АЕ=DC, AD=BE,
Ð ADC = Ð DEC. Найдите длину ЕС.
7.4. Последовательность чисел строится по следующему закону.
На первом месте стоит число 7, далее за каждым числом стоит сумма
цифр его квадрата, увеличенная на единицу. Например, на втором месте
стоит число 14, так как 72=49, а 4+9+1=14.
На третьем месте стоит число 17 и так далее.
Какое число стоит на 2005-м месте?
7.5. На поле для игры в "морской бой" размером 10´10 клеток
поставили корабль размером 1´3.
Можно ли, сделав 33 выстрела, наверняка в него попасть? Решения.
7.1. Ответ: да, существуют: 1/2 и -1.
7.2. Ответ: нет, не сможет.
Для того, чтобы средняя скорость гонца, пробежавшего 24 мили,
была равна 12 милям в час, необходимо, чтобы он пробежал этот путь за 2 часа.
Но из условия следует, что за два часа гонец пробежал только 16 миль.
7.3. Ответ: ЕС = 1 см.
7.4. Ответ: 11.
7.5. Ответ: да, можно.
8 класс
8.1. Корень из числа 49 можно извлечь по такой "формуле": 8.2. Решите уравнение:
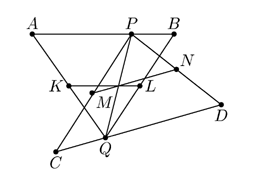
8.3. Отрезки AB и CD не параллельны и не пересекаются.
Точка P лежит на отрезке AB, а точка Q — на отрезке CD.
Точки K, L, M и N — середины отрезков AQ, BQ, CP и DP соответственно.
Докажите, что отрезки KL, MN и PQ пересекаются в одной точке.
8.4. Какое наименьшее количество клеток квадрата 5´5 нужно закрасить,
чтобы в любом квадрате 3´3, являющемся его частью,
было ровно 4 закрашенных клетки?
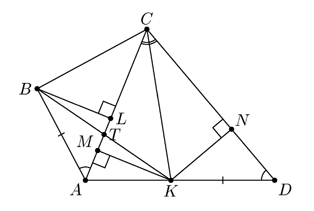
8.5. В выпуклом четырёхугольнике ABCD углы BAC и ADC равны.
CK — биссектриса треугольника ACD.
Докажите, что если KD=AB, то прямая AC делит отрезок KB пополам.
8.6. К Пете на день рождения пришло несколько гостей. На столе стояла большая
ваза с конфетами. Один из гостей подошел к вазе, мысленно поделил конфеты на всех
поровну (включая Петю), взял свою долю и ещё одну конфету.
Второй гость, подойдя к вазе, также мысленно поделил оставшиеся конфеты на всех
присутствующих, взял свою долю и ещё две конфеты.
Аналогично поступил третий гость (взяв дополнительно три конфеты), и так далее.
Последним к вазе подошёл Петя и обнаружил, что она пуста.
Докажите, что все гости получили конфет поровну. Решения.
8.1. Ответ: да, существуют: 64 и 81.
8.2. Ответ: -4.
8.3. Ответ: Из условия следует, что KL — средняя линия треугольника AQB, то есть, KL||AB (см. рисунок).
По теореме Фалеса KL проходит через середину отрезка PQ .
Аналогично, из того, что MN — средняя линия треугольника CPD следует, что и отрезок MN
проходит через середину отрезка PQ .
8.4. Ответ: 7 клеток.
8.5. Ответ: Рассмотрим случай, когда углы BAC и ADC острые (см. рисунок).
Пусть T — точка пересечения прямой AC и отрезка BK . Проведём
перпендикуляры KM и KN к прямым CA и CD соответственно. Так как CK —
биссектриса треугольника, то KM=KN . Проведем также перпендикуляр BL к
прямой AC . Тогда прямоугольные треугольники ABL и DKN равны по гипотенузе
и острому углу. Следовательно, BL=KN=KM . Поэтому прямоугольные треугольники
BLT и KMT равны по катету и острому углу, откуда следует, что BT=KT, что
и требовалось доказать.
8.6. Ответ: Пусть к Пете пришло N гостей. Найдем, сколько конфет взял последний гость.
Пусть к моменту подхода к вазе последнего гостя в ней было X конфет. Этот гость
взял X/(N+1)+N конфет, забрав при этом все конфеты, то есть X=X/(N+1)+N,
откуда X=N+1.
9 класс
9.1. Существует ли такой набор натуральных чисел, что их сумма равна
2005 и их произведение также равно 2005?
9.2. Рассматриваются функции вида y=x2+ax+b, где a+b=2005. Докажите, что
графики всех таких функций имеют общую точку.
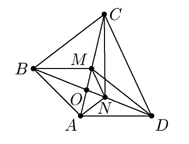
9.3. На диагоналях AC и BD выпулого четырёхугольника ABCD взяты точки M и N
соответственно так, что MB||AD и NA||BC. Докажите, что MN||CD.
9.4. На острове рыцарей и лжецов (лжецы всегда лгут, рыцари
всегда говорят правду) каждый болеет ровно за одну футбольную команду.
В опросе приняли участие все жители острова.
На вопрос "Болеете ли Вы за "Спартак"?" ответили "Да" 40% жителей. На аналогичный
вопрос про "Зенит" утвердительно ответили 30%, про "Локомотив" — 50%,
а про ЦСКА — 0%. Какой процент жителей острова действительно болеет за "Спартак"?
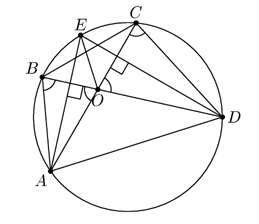
9.5. Четырёхугольник ABCD вписан в окружность. O — точка пересечения
его диагоналей, E — середина дуги BC, не содержащей точек A и D.
Докажите, что если AO=AB, то EO_|_ AD.
9.6. По кругу записано n целых чисел, сумма которых равна 14. Известно, что
любое из записанных чисел равно модулю разности двух чисел, следующих за ним.
Найдите все возможные значения n. Решения.
9.1. Ответ: да, существует.
9.2. y(1)=1+a+b=2006 . Следовательно, каждый из данных графиков
проходит через точку с координатами (1; 2006).
9.3. Ответ: Пусть O — точка пересечения диагоналей четырёхугольника. Тогда точка
M лежит на отрезке
OC, а точка N — на отрезке OD . В трапеции (или параллелограмме) ABMD
OB:OD=OM:OA.
Аналогично, в трапеции (или параллелограмме) ANCB ON:OB=OA:OC.
Перемножая эти равенства почленно, получим ON:OD=OM:OC.
Следовательно, треугольники MON и COD подобны, то есть MN||CD .
9.4. Ответ: 30% .
9.5. ÐDCA=ÐABD
(вписанные, опирающиеся на одну дугу, см. рисунок).
Из того, что AB=AO, следует, что ÐABD=ÐAOB=ÐCOD.
Следовательно, треугольник CDO равнобедренный с основанием OC .
Так как точка E — середина дуги BC, то она лежит на биссектрисах
вписанных углов BAC и CDB . Так как треугольники BAO и CDO
равнобедренные, то AE_|_OB, DE_|_OC . Рассмотрим треугольник AOD .
Две его высоты лежат на прямых AE и DE, то есть E — точка пересечения
высот треугольника. Следовательно, третья высота треугольника лежит на прямой EO, то есть
EO_|_AD.
9.6. Ответ: n=3 или n=21 .
10 класс
10.1. Решите уравнение
10.2. (аn) — арифметическая прогрессия с разностью 1.
Известно, что S2005 — наименьшая среди всех Sn
(меньше суммы первых n членов для любого другого значения n).
Какие значения может принимать первый член прогрессии?
10.3. Два равных квадрата со стороной 20 имеют общий центр.
Докажите, что площадь их общей части не меньше, чем 314.
10.4. Все пятизначные числа, составленные из цифр от 1 до 5 без повторений,
занумерованы в порядке возрастания. Какой номер имеет число 43521?
10.5. Можно ли, пользуясь только операциями сложения, вычитания и умножения,
составить из выражений 3х2 + х и 3х выражение, тождественно равное х?
10.6. В треугольнике ABC рассматриваются все отрезки, соединющие вершины
треугольника с точками на противолежащей стороне (включая стороны
треугольника). Для каких треугольников ABC cуществует точка О в пространстве,
из которой все рассматриваемые отрезки видны под одинаковыми углами? Решения.
10.1. Ответ: 249999.
10.2. Ответ: а1 принадлежит интервалу (-2005; -2004).
10.3. В пересечении квадратов получается многоугольник, стороны
которого удалены от центра квадратов на расстояние 10.
Следовательно, в этот многоугольник можно вписать круг.
10.4. Ответ: номер 90.
10.5. Ответ: нет, нельзя.
10.6. Ответ: для остроугольных треугольников.
Первый способ. Произведение данных чисел должно оканчиваться цифрой 1.
Второй способ. Произведение двух нечётных чисел должно быть нечётным.
Третий способ. Первое число больше, чем 400000, второе — больше, чем 8000,
поэтому произведение должно быть больше, чем 3200000000.
Так как в детский сад может ходить
только пятилетний ребёнок, то самый младший ребёнок — девочка.
Значит, Мише — не пять лет. Аня старше Миши, то есть Ане исполнилось либо 13,
либо 15 лет. Так как сумма возрастов Ани и Жени
делится на три, то Ане не может быть пятнадцать лет.
Следовательно, Ане — тринадцать. Миша её младше, значит, Мише —
восемь. Тогда Жене пять лет и она девочка.
Сумма чисел, записанных Васей, равна пяти, поэтому Ваня записал число 10.
Следовательно, сумма всех чисел равна 5+5+10=20.
Разобьём таблицу на 16 квадратов 2´2.
Тогда хотя бы в одном из этих квадратов окажется не менее
двух закрашеных клеток, и эти клетки будут соседними.
1.2. Обязательно нужно наклеить марку на второй конверт.
2.2. Необходимо наклеить марку на третий конверт.
3.2. Требуется наклеить марку на первый конверт.
Второй способ. Пусть x — цена взрослой путевки.
Тогда по условию задачи можно составить уравнение 3x-500=3543 .
Это уравнение не имеет натуральных решений.
Решение удобно записать в виде таблицы:
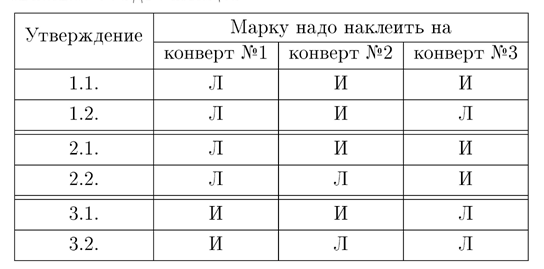
Таким образом, условие задачи будет выполнено только в случае, если марка будет
наклеена на третий конверт.
Запишем пример в столбик:
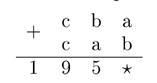
Сумма двух одинаковых цифр в разряде
сотен чётна, поэтому сумма цифр b и a больше 10, то есть равна 14.
Поэтому цифра a не может быть меньше 5.
Несложно убедиться, что a может принимать все значения от 5 до 9.
До встречи Печкин проехал путь, в шесть раз больший,
чем прошел Матроскин. К тому времени, когда Печкин вернулся обратно,
Матроскин прошел еще столько же, сколько до встречи.
Следовательно, за 30 минут ему осталось пройти в пять раз больше,
чем было им пройдено до встречи.
То есть, до встречи с Печкиным Матроскин шел 6 минут.
Следовательно, на весь путь он потратил 6+6*6=42 (мин).
Действительно, 1/2+(-1)=(1/2)*(-1)=(1/2):(-1).
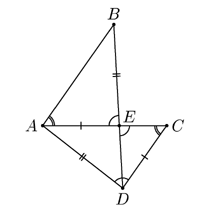
Так как AD = BE ; CD = AE ; ÐADC =ÐDEC =Ð
BEA (вертикальные углы),
то Δ ADC = Δ BEA
(см. рисунок). Из равенства этих треугольников следует,
что АС = АВ, тогда ЕС =АС - АЕ = АВ - АЕ = 1 см (по условию).
Вычислим несколько первых членов данной последовательности:
7; 14; 17; 20; 5; 8; 11; 5; 8; 11; 5; ...
Таким образом, начиная с пятого члена последовательности,
будет повторяться одна и та же тройка чисел 5, 8, 11.
Так как 2005-4=2001, а 2001 кратно 3, то на 2005-м месте
будет стоять число 11.
Например, если сделать 33 выстрела в клетки, отмеченные на рисунке.
.
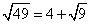Существуют ли другие двузначные числа, квадратные корни из которых извлекаются
аналогичным образом и являются целыми? Укажите все такие двузначные числа.
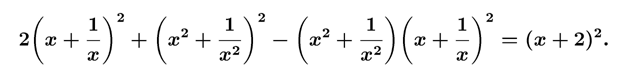
Рассмотрим все двузначные числа,
являющиеся квадратами целых чисел. Корни из чисел 16, 25 и 36
не могут быть извлечены указанным способом, так как квадратные корни
из их последних цифр не являются целыми. Числа 49, 64 и 81 являются
решениями.
При x отличном от 0
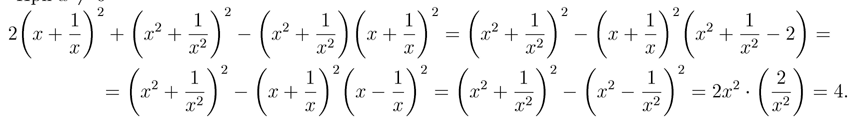
Решая уравнение (x+2)2=4, получим, что x=-4 или x=0 . При x=0 левая часть
уравнения не имеет смысла.
Покажем, что придётся закрасить не менее семи клеток. Рассмотрим два квадрата 3´3
(см. рисунок слева).
В каждом из этих квадратов должно быть закрашено по четыре клетки. Так как их общая часть составляет
одну клетку, то в них не может быть закрашено менее семи клеток.
Один из возможных примеров с семью закрашенными клетками приведён на рисунке справа.
Случаи, когда углы BAC и ADC прямые или тупые,
рассматриваются аналогично.
Аналогично, пусть к моменту подхода к вазе предпоследнего гостя
в ней было Z конфет. Этот гость
взял Z/(N+1)+N-1 конфет,
оставив при этом N+1 конфету, то есть Z-Z/(N+1)+N-1=N+1,
откуда Z=2(N+1) . Таким образом, предпоследний гость также взял N+1 конфету.
Рассуждая аналогично, можно доказать, что каждый гость взял по (N+1)-ой конфете.
Более строго это рассуждение можно провести следующим образом.
Докажем индукцией по k следующее утверждение: "К моменту
подхода к вазе (N+1-k)-го гостя в вазе находилось k(N+1) конфет". База индукции:
k=1 — доказана выше. Проведём шаг индукции. Пусть утверждение верно
для k=s, докажем, что оно верно для k=s+1 . Пусть к моменту подхода к вазе (N+1-s-1)-го
гостя в ней было Y конфет. Он взял Y/(N+1)+N-s конфет, после чего в вазе
осталось Y-Y/(N+1)+N-s конфет, что по предположению индукции равно s(N+1) .
Из уравнения Y-Y/(N+1)+N-s=l(N+1) получим, что y=(s+1)(N+1) . Утверждение
доказано.
Например, числа 5, 401 и 1599 единиц.
Пусть x% жителей острова составляют лжецы. Тогда (100-x)% составляют рыцари.
Так как каждый рыцарь утвердительно ответил ровно на один из вопросов, а
каждый лжец — на три, то (100-x)+3x=40+30+50, откуда x=10.
Так как ни один из жителей острова не сказал, что болеет за ЦСКА,
то все лжецы болеют за ЦСКА. Каждый из них заявил, что болеет за "Спартак",
поэтому действительно болеют за
"Спартак" 40%-10%=30% жителей.
Из условия следует, что все записанные числа неотрицательны. Пусть a —
наибольшее из этих чисел (если таких несколько, то выберем любое из них);
b, c, d и e — числа, следующие за ним по кругу. По условию a=|b-c|, что
возможно, только если одно из чисел b или c равно a, а другое равно
нулю. Если b=a, c=0, то d=e=a и так далее.
Если же b=0, c=a, то d=a, e=0 и так далее.
Таким образом, записанные
числа таковы: a, a, 0, a, a, 0,...,a, a, 0. Их сумма равна 2ma, где m — количество нулей.
Из равенства 2ma=14 следует, что ma=7, то есть либо m=7, a=1, либо
m=1, a=7 . Следовательно, n=21 или n=3 .
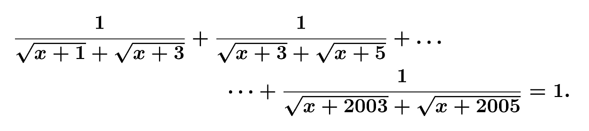
Умножим числитель и знаменатель каждой дроби на выражение, сопряжённое знаменателю:
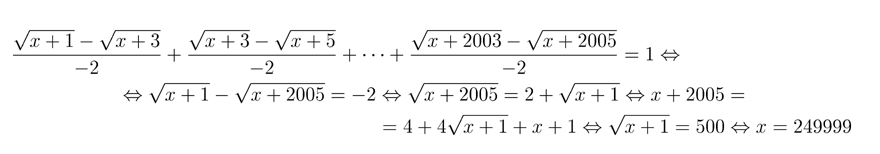
Так как разность прогрессии положительна, то прогрессия — возрастающая.
Следовательно, описанная ситуация возможна тогда и только тогда, когда члены
прогрессии с первого по 2005-ый — отрицательны, а начиная с 2006-ого — положительны.
Таким образом, S_{2005} будет наименьшей, тогда и только тогда, когда а2005<0,
а а2006>0 . Отсюда получаем систему
неравенств
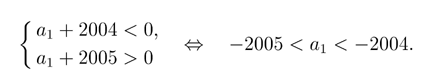
Площадь этого круга равна 100p>314 .
Следовательно, площадь общей части квадратов больше, чем 314.
Все числа, начинающиеся с цифр 1, 2 или 3, меньше данного числа.
Тогда на остальных местах цифры могут стоять в произвольном порядке,
то есть их в каждом случае по 4! Значит, чисел,
начинающихся с 1, 2 или 3, в точности 3* 4!=72 .
Кроме того, меньше данного будут все числа, начинающиеся с 41 или 42.
Таких чисел будет 2*3! = 12 . Чисел, начинающихся с 431 или 432 будет
2*2! = 4, и они также меньше данного.
И еще одно число, меньшее данного: 43512.
Итого 72+12+4+1=89 чисел. Следовательно, данное число имеет номер 90.
Предположим, что составить выражение, тождественно равное х, можно,
то есть для всеx x выполняется равенство f(3x2 + x; 3x)=x .
Но при х = 2/3 3x2+x=3x=2, следовательно, левая часть равенства
принимает целое значения, а правая— дробное (равна 2/3 ).
Рассмотрим треугольник ABC и точку O, удовлетворяющие условию.
1) Докажем, что точка O не может лежать в плоскости треугольника.
Действительно, если точка O лежит в плоскости ABC, то из равенства углов
Ð AOB, Ð BOC и
Ð COA следует,
что она лежит внутри треугольника. Поэтому каждая
сторона треугольника видна из неё под углом, меньшим 180o, а,
например, отрезок AD, проходящий через точку O — под углом 180o.
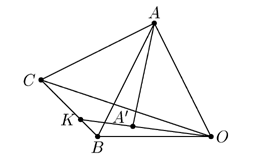
2) Докажем, что Ð AOB=Ð BOC=Ð COA=90o.
Пусть это не так. Предположим, что эти углы— острые (cм. рисунок слева).
Пусть точка A' — проекция точки A на плоскость BOC .
Тогда, так как Ð AOB=Ð AOC, то OA' — биссектриса
Ð BOC, пересекающая отрезок BC в точке K .
Ð AOK — это угол между прямой AO и плоскостью BOC,
поэтому Ð AOK<Ð AOC . Следовательно, отрезки AK и AC видны
из точки O под разными углами. Случай тупых углов рассматривается аналогично.
3) Докажем, что треугольник ABC может быть только остроугольным.
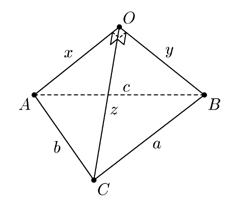
Пусть BC=a, CA=b, AB=c, OA=x, OB=y, OC=z (см. рисунок справа). Тогда
то есть треугольник ABC остроугольный.
4) Заметим, что если треугольник ABC остроугольный, то рассмотренная система
уравнений всегда имеет положительные решения (x, y, z), то есть существует точка O,
из которой его стороны видны под прямыми углами. Докажем, что из этой точки
каждый из остальных рассматриваемых отрезков виден под прямым углом.
Действительно, так как OA_|_OB и OA_|_OC, то OA_|_(OBC).
Следовательно, прямая OA перпендикулярна любой прямой, лежащей в этой
плоскости. Поэтому для любой точки M, лежащей на отрезке BC, Ð AOM=90o.
Аналогично, OB_|_(AOC) и OC_|_(AOB).
