8 класс
Задача 1. Учительница продиктовала Вовочке угловые коэффициенты и свободные члены трёх разных линейных функций, графики которых параллельны. Невнимательный Вовочка при записи каждой из функций поменял поменял местами угловой коэффициент и свободный член и построил графики получившихся функций. Сколько могло получиться точек, через которые проходят хотя бы два графика?
Задача 2. На урок физкультуры пришло 12 детей, все разной силы. Учитель 10 раз делил их на две команды по 6 человек, каждый раз новым способом, и проводил состязание по перетягиванию каната. Могло ли оказаться так, что все 10 раз состязание закончилось вничью (то есть суммы сил детей в командах были равны)?
Задача 3. Плоскость разбита на части несколькими прямыми, среди которых есть непараллельные. Те части, граница которых состоит из двух лучей, закрасили. После этого проведена ещё одна прямая. Докажите, что, независимо от положения новой прямой, по обе стороны от неё найдутся закрашенные точки.
Пример расположения прямых (без последней прямой) изображен на рисунке.

Задача 4. На боковых сторонах $AB$ и $BC$ равнобедренного остроугольного треугольника $ABC$ выбраны точки $M$ и $K$. Отрезки $CM$ и $AK$ пересекаются в точке $E$. Оказалось, что $\angle MEA = \angle ABC$. Докажите, что середины всевозможных отрезков $MK$ лежат на одной прямой.
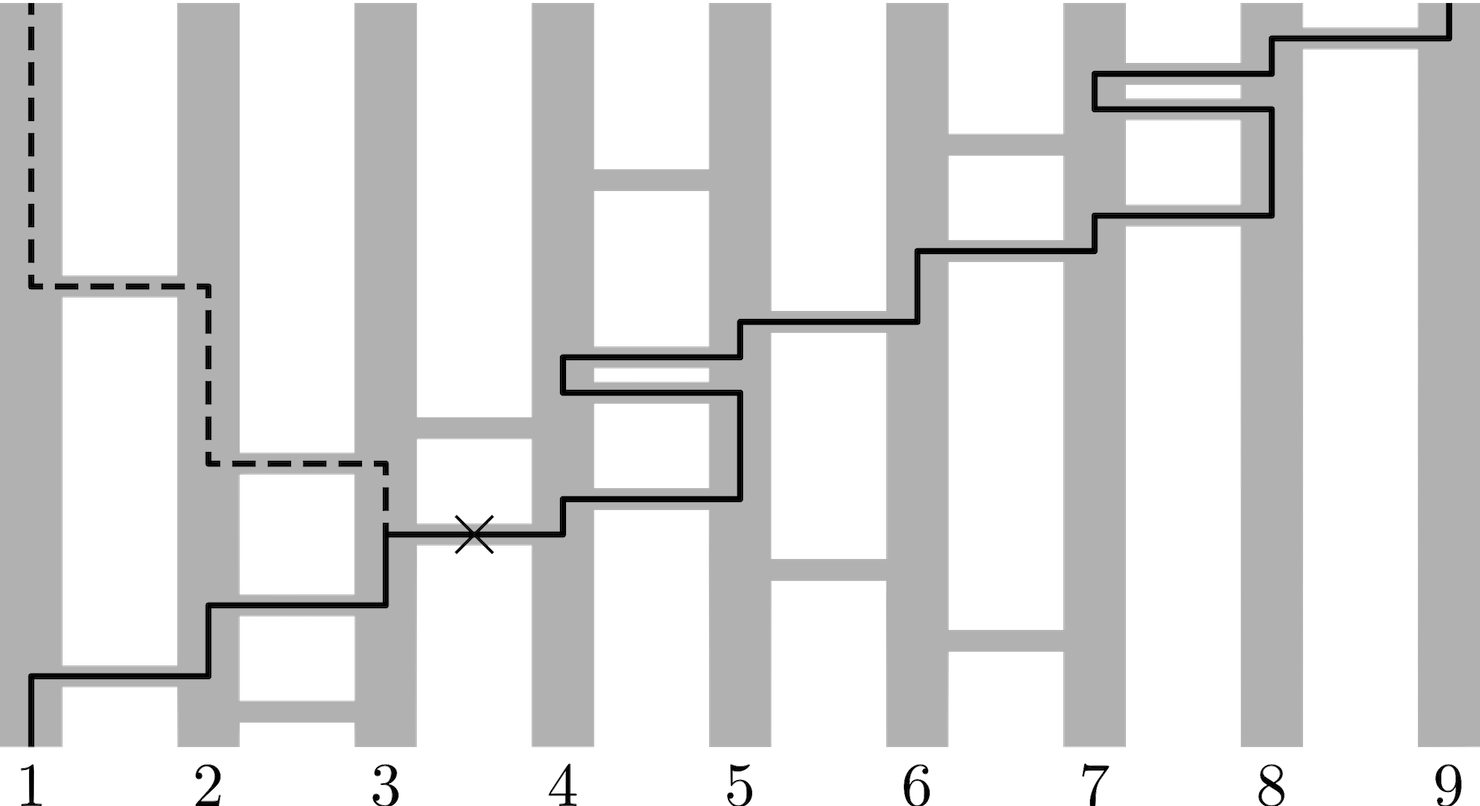
Задача 5. В ряд стоят 9 вертикальных столбиков. В некоторых местах между соседними столбиками вставлены горизонтальные палочки, никакие две из которых не находятся на одной высоте. Жук ползёт снизу вверх; когда он встречает палочку, он переползает по ней на соседний столбик и продолжает ползти вверх. Известно, что если жук начинает внизу первого столбика, то он закончит свой путь на девятом столбике. Всегда ли можно убрать одну из палочек так, чтобы жук, начав внизу первого столбика, в конце пути оказался наверху пятого столбика?
Например, если палочки расположены как на рисунке, то жук будет ползти по сплошной линии. Если убрать третью палочку на пути жука, то он поползёт по пунктирной линии.
Задача 6. Вася выбрал $100$ различных натуральных чисел из множества ${1, 2, 3, \ldots, 120}$ и расставил их в некотором порядке вместо звёздочек в выражении (всего $100$ звёздочек и $50$ знаков корня) $$ \sqrt{(* + *)\cdot \sqrt{(* + *) \cdot \sqrt{ \ldots \sqrt{*+*}}}}. $$ Могло ли значение полученного выражения оказаться целым числом?
9 класс
Задача 1. Действительные числа $a$, $b$, $c$, $d$ таковы, что $$ \frac{a}{b} + \frac{b}{a} = \frac{c}{d} + \frac{d}{c}. $$ Докажите, что произведение каких-то двух чисел из $a$, $b$, $c$, $d$ равно произведению двух других.
Задача 2. На урок физкультуры пришло 12 детей, все разной силы. Учитель 10 раз делил их на две команды по 6 человек, каждый раз новым способом, и проводил состязание по перетягиванию каната. Могло ли оказаться так, что все 10 раз состязание закончилось вничью (то есть суммы сил детей в командах были равны)?
Задача 3. Петя загадал положительную несократимую дробь $x = \frac{m}{n}$. За один ход Вася называет положительную несократимую дробь $y$, не превосходящую 1, и Петя в ответ сообщает Васе числитель несократимой дроби, равной сумме $x+y$. Как Васе за два хода гарантированно узнать $x$?
Задача 4. На описанной окружности треугольника $ABC$ отметили середины дуг $BAC$ и $CBA$ — точки $M$ и $N$ соответственно, и середины дуг $BC$ и $AC$ — точки $P$ и $Q$ соответственно. Окружность $\omega_1$ касается стороны $BC$ в точке $A_1$ и продолжений сторон $AC$ и $AB$. Окружность $\omega_2$ касается стороны $AC$ в точке $B_1$ и продолжений сторон $BA$ и $BC$. Оказалось, что $A_1$ лежит на отрезке $NP$. Докажите, что $B_1$ лежит на отрезке $MQ$.
Задача 5. В ряд стоят $9$ вертикальных столбиков. В некоторых местах между соседними столбиками вставлены горизонтальные палочки, никакие две из которых не находятся на одной высоте. Жук ползёт снизу вверх; когда он встречает палочку, он переползает по ней на соседний столбик и продолжает ползти вверх. Известно, что если жук начинает внизу первого столбика, то он закончит свой путь на девятом столбике. Всегда ли можно убрать одну из палочек так, чтобы жук, начав внизу первого столбика, в конце пути оказался наверху пятого столбика?
Например, если палочки расположены как на рисунке, то жук будет ползти по сплошной линии. Если убрать третью палочку на пути жука, то он поползёт по пунктирной линии.

Задача 6. На каждой из 99 карточек написано действительное число. Все 99 чисел различны, а их общая сумма иррациональна. Стопка из 99 карточек называется неудачной, если для каждого натурального $k$ от 1 до 99 сумма чисел на $k$ верхних карточках иррациональна. Петя вычислил, сколькими способами можно сложить исходные карточки в неудачную стопку. Какое наименьшее значение он мог получить?
10 класс
Задача 1. Петя и Вася играют на отрезке $[0;1]$, в котором отмечены точки $0$ и $1$. Игроки ходят по очереди, начинает Петя. Каждый ход игрок отмечает ранее не отмеченную точку отрезка. Если после хода очередного игрока нашлись три последовательных отрезка между соседними отмеченными точками, из которых можно сложить треугольник, то сделавший такой ход игрок объявляется победителем, и игра заканчивается. Получится ли у Пети гарантированно победить?
Задача 2. Докажите, что среди вершин выпуклого девятиугольника можно найти три, образующие тупоугольный треугольник, ни одна сторона которого не совпадает со сторонами девятиугольника.
Задача 3. В клуб любителей гиперграфов в начале года записались $n$ попарно незнакомых школьников. За год клуб провёл $100$ заседаний, причём каждое заседание посетил хотя бы один школьник. Два школьника знакомились, если было хотя бы одно заседание, которое они оба посетили. В конце года оказалось, что количество знакомых у каждого школьника не меньше, чем количество заседаний, которые он посетил. Найдите минимальное значение $n$, при котором такое могло случиться.
Задача 4. Дан описанный четырёхугольник $ABCD$ с тупым углом $ABC$. Лучи $AB$ и $DC$ пересекаются в точке $P$, а лучи $DA$ и $CB$ — в точке $Q$. Докажите, что $|AD - CD| \geqslant |r_1 - r_2|$, где $r_1$ и $r_2$ — радиусы вписанных окружностей треугольников $PBC$ и $QAB$.
Задача 5. Будем называть натуральное число $N$ сильно кубическим, если существует такой приведённый кубический многочлен $f(x)$ с целыми коэффициентами, что $f(f(f(N))) = 0$, а $f(N)$ и $f(f(N))$ не равны 0. Верно ли, что все числа, большие $20^{24}$, сильно кубические?
Задача 6. На каждой из 99 карточек написано действительное число. Все 99 чисел различны, а их общая сумма иррациональна. Стопка из 99 карточек называется неудачной, если для каждого натурального $k$ от 1 до 99 сумма чисел на $k$ верхних карточках иррациональна. Петя вычислил, сколькими способами можно сложить исходные карточки в неудачную стопку. Какое наименьшее значение он мог получить?
11 класс (1 день)
Задача 1. У математика есть 19 различных гирь, массы которых в килограммах равны $\ln 2$, $\ln 3$, $\ln 4$, …, $\ln 20$, и абсолютно точные двухчашечные весы. Он положил несколько гирь на весы так, что установилось равновесие. Какое наибольшее число гирь могло оказаться на весах?
Задача 2. В остроугольном треугольнике $ABC$ проведена высота $AH$. Точки $M$ и $N$ — середины отрезков $BH$ и $CH$. Докажите, что точка пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, равноудалена от точек $B$ и $C$.
Задача 3. Имеется кучка из 100 камней. Двое играют в следующую игру. Первый игрок забирает 1 камень, потом второй может забрать 1 или 2 камня, потом первый может забрать 1, 2 или 3 камня, затем второй 1, 2, 3 или 4 камня, и так далее. Выигрывает тот, кто забирает последний камень. Кто может выиграть, как бы ни играл соперник?
Задача 4. Дан многочлен степени $n \geqslant 1$ с целыми ненулевыми коэффициентами, каждый из которых является его корнем. Докажите, что модули всех коэффициентов этого многочлена не превосходят 2.
Задача 5. В тетраэдре $ABCD$ скрещивающиеся рёбра попарно равны. Через середину отрезка $AH_A$, где $H_A$ — точка пересечения высот грани $BCD$, провели прямую $h_A$ перпендикулярно плоскости $BCD$. Аналогичным образом определили точки $H_B$, $H_C$, $H_D$ и построили прямые $h_B$, $h_C$, $h_D$ соответственно для трёх других граней тетраэдра. Докажите, что прямые $h_A$, $h_B$, $h_C$, $h_D$ пересекаются в одной точке.
Задача 6. Кощей придумал для Ивана-дурака испытание. Он дал Ивану волшебную дудочку, на которой можно играть только две ноты — до и си. Для прохождения испытания Ивану нужно сыграть какую-нибудь мелодию из 300 нот на свой выбор. Но до того, как он начнёт играть, Кощей выбирает и объявляет запретными одну мелодию из пяти нот, одну — из шести нот, …, одну — из 30 нот. Если в какой-то момент последние сыгранные ноты образуют одну из запретных мелодий, дудочка перестаёт звучать. Сможет ли Иван пройти испытание, какие бы мелодии Кощей ни объявил запретными?
11 класс (2 день)
Задача 1. Существует ли на координатной плоскости точка, относительно которой симметричен график функции $f(x)=\dfrac{1}{2^x+1}$?
Задача 2. Чемпионат по футболу проходил в два круга. В каждом круге каждая команда сыграла с каждой один матч (за победу даётся три очка, за ничью одно, за поражение ноль). Оказалось, что все команды вместе набрали в первом круге 60% от общей суммы всех очков за два круга. Известно также, что победитель чемпионата набрал во втором круге в 30 раз меньше очков, чем все команды вместе в первом круге. Сколько команд участвовало в турнире?
Задача 3. Докажите, что если при $n\in\mathbb{N}$ число $2+2\sqrt{12n^2+1}$ целое, то оно — точный квадрат.
Задача 4. В остроугольном треугольнике $ABC$ высоты $AH_A$, $BH_B$ и $CH_C$ пересекаются в точке $H$. Через точки, в которых окружность радиуса $HH_A$ с центром $H$ пересекает отрезки $BH$ и $CH$, проведена прямая $\ell_A$. Аналогично проведены прямые $\ell_B$ и $\ell_C$. Докажите, что точка пересечения высот треугольника, образованного прямыми $\ell_A,\,\ell_B,\,\ell_C$, совпадает с центром окружности, вписанной в треугольник $ABC$.
Задача 5. Петя и Вася независимо друг от друга разбивают белую клетчатую доску $100\times 100$ на произвольные группы клеток, каждая из чётного (но не обязательно все из одинакового) числа клеток, каждый — на свой набор групп. Верно ли, что после этого всегда можно покрасить по половине клеток в каждой группе из разбиения Пети в чёрный цвет так, чтобы в каждой группе из разбиения Васи было поровну чёрных и белых клеток?