5.1. В примере на сложение двух чисел первое слагаемое меньше суммы на 2000, а сумма больше второго слагаемого на 6. Восстановите пример.
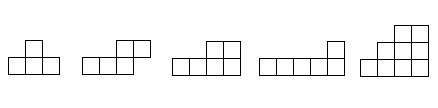
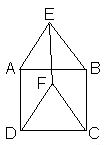
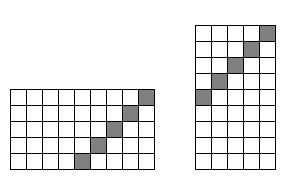
5.2. Составьте квадрат, используя ровно четыре из пяти изображенных ниже фигур. Каждую из четырех выбранных Вами фигур можно использовать только один раз.
5.3. Без ореха (от дупла до орешника) белка бежит со скоростью 4 м/сек, а с орехом (от орешника до дупла) — со скоростью 2 м/сек. На путь от дупла до орешника и обратно она тратит 54 секунды. Найдите расстояние от дупла до орешника. Ответ обоснуйте.
5.4. В день рождения дяди Федора почтальон Печкин хочет выяснить, сколько тому лет. Шарик говорит, что дяде Федору больше 11 лет, а кот Матроскин утверждает, что больше 10 лет. Сколько лет дяде Федору, если известно, что ровно один из них ошибся? Ответ обоснуйте.
5.5. В забеге от Воробьевых гор до Красной площади приняли участие три спортсмена.
Сначала стартовал Гриша, затем — Саша, и последней — Лена. После финиша выяснилось, что
во время забега Гриша обгонял других 10 раз, Лена — 6 раз, Саша — 4 раза,
причем все трое ни разу не оказывались в одной точке одновременно.
В каком порядке финишировали спортсмены, если известно, что они пришли к финишу в разное время?
Ответ обоснуйте.
Решения.
5.1. Ответ: 6+2000 = 2006.
Если из суммы двух чисел вычесть одно из слагаемых, то получится другое слагаемое.
Из условия следует, что второе слагаемое равно 2000, а первое - равно 6.
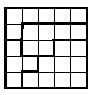
5.2. Ответ: cм. рисунок.
Можно определить длину стороны искомого квадрата.
Общее количество клеток пяти фигур равно 4+5+6+6+9=30.
Значит, если можно составить квадрат, то только со стороной 5.
Таким образом, лишней является фигура из пяти клеток.
5.3. Ответ: 72 метра.
Поскольку обратно белка бежит в два раза медленнее, то
время, затраченное белкой на обратную дорогу, в два раза больше времени, которое она тратит
на дорогу от дупла до орешника.
Поэтому, время, затраченное на дорогу от дупла до орешника, в три раза меньше
времени, затраченного на всю дорогу, то есть, равно 54 : 3 = 18 секунд.
Следовательно, расстояние от дупла до орешника равно 18*4 = 72 метра.
5.4. Ответ: дяде Федору 11 лет.
Заметим, что если не ошибся Шарик, то не ошибся и Матроскин, что противоречит условию.
Значит, Шарик сказал неправду, в отличие от кота Матроскина.
Таким образом, дяде Федору больше 10 лет, но не меньше 11.
Следовательно, дяде Федору исполнилось 11 лет.
5.5. Ответ: первым финишировал Гриша, затем - Саша, и последней - Лена.
Гриша стартовал первым. Чтобы он смог совершить 10 обгонов, необходимо
чтобы Саша и Лена обогнали его хотя бы 10 раз.
Так как общее количество обгонов Саши и Лены равно 6 + 4 = 10, то они обгоняли только
Гришу и не обгоняли друг друга. После того, как Гриша совершил все 10 обгонов, он опять оказался
первым. Значит, спортсмены финишировали в том же порядке, в котором и стартовали.
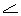 ACD равен 90o.
ACD равен 90o.
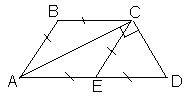
 .
.
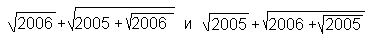 .
.
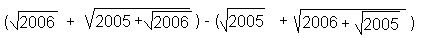 =
=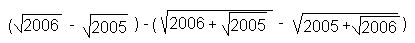 =
=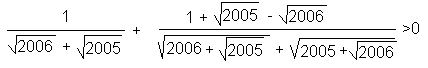 ,
,
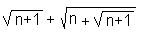 и B=
и B=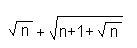 .
Поскольку оба числа положительны, то достаточно сравнить их квадраты:
.
Поскольку оба числа положительны, то достаточно сравнить их квадраты:
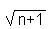 +2
+2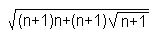 ,
,
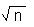 +2
+2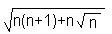 .
.
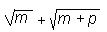 —
также натуральное число.
—
также натуральное число.
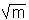 +
+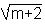 - натуральное число. Тогда
- натуральное число. Тогда